Non-monotonic Extensions to Formal Concept Analysis via Object Preferences

Formal Concept Analysis (FCA) is an approach to creating a conceptual hierarchy in which a \textit{concept lattice} is generated from a \textit{formal context}. That is, a triple consisting of a set of objects, $G$, a set of attributes, $M$, and an incidence relation $I$ on $G \times M$. A \textit{concept} is then modelled as a pair consisting of a set of objects (the \textit{extent}), and a set of shared attributes (the \textit{intent}). Implications in FCA describe how one set of attributes follows from another. The semantics of these implications closely resemble that of logical consequence in classical logic. In that sense, it describes a monotonic conditional. The contributions of this paper are two-fold. First, we introduce a non-monotonic conditional between sets of attributes, which assumes a preference over the set of objects. We show that this conditional gives rise to a consequence relation that is consistent with the postulates for non-monotonicty proposed by Kraus, Lehmann, and Magidor (commonly referred to as the KLM postulates). We argue that our contribution establishes a strong characterisation of non-monotonicity in FCA. Typical concepts represent concepts where the intent aligns with expectations from the extent, allowing for an exception-tolerant view of concepts. To this end, we show that the set of all typical concepts is a meet semi-lattice of the original concept lattice. This notion of typical concepts is a further introduction of KLM-style typicality into FCA, and is foundational towards developing an algebraic structure representing a concept lattice of prototypical concepts.

Towards Propositional KLM-Style Defeasible Standpoint Logics

The KLM approach to defeasible reasoning introduces a weakened form of implication into classical logic. This allows one to incorporate exceptions to general rules into a logical system, and for old conclusions to be withdrawn upon learning new contradictory information. Standpoint logics are a group of logics, introduced to the field of Knowledge Representation in the last 5 years, which allow for multiple viewpoints to be integrated into the same ontology, even when certain viewpoints may hold contradicting beliefs. In this paper, we aim to integrate standpoints into KLM propositional logic in a restricted setting. We introduce the logical system of Defeasible Restricted Standpoint Logic (DRSL) and define its syntax and semantics. Specifically, we integrate ranked interpretations and standpoint structures, which provide the semantics for propositional KLM and propositional standpoint logic respectively, in order to introduce ranked standpoint structures for DRSL. Moreover, we extend the non-monotonic entailment relation of rational closure from the propositional KLM case to the DRSL case. The main contribution of this paper is to characterize rational closure for DRSL both algorithmically and semantically, showing that rational closure can be characterized through a single representative ranked standpoint structure. Finally, we conclude that the semantic and algorithmic characterizations of rational closure are equivalent, and that entailment-checking for DRSL under rational closure is in the same complexity class as entailment-checking for propositional KLM.

Enriching Ontologies with Disjointness Axioms using Large Language Models

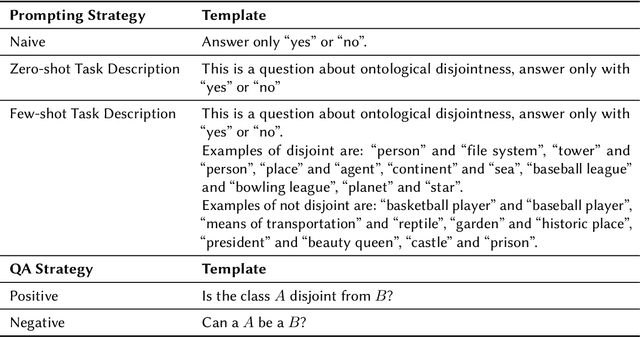
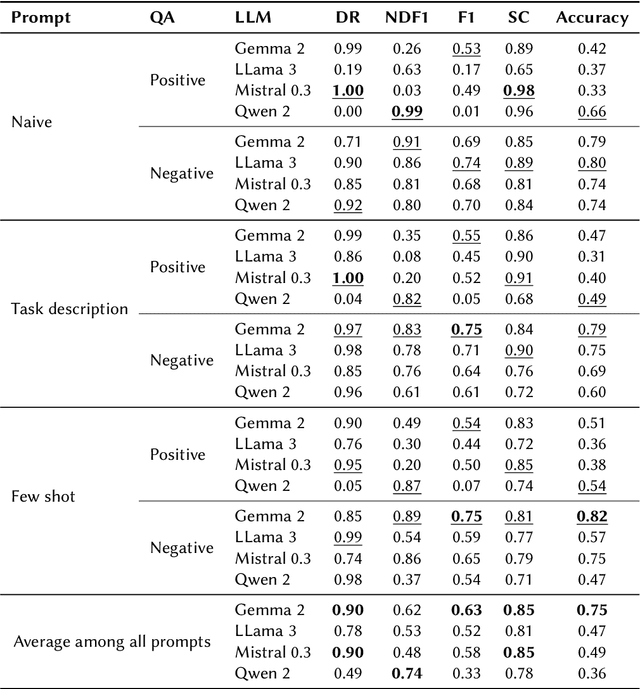
Ontologies often lack explicit disjointness declarations between classes, despite their usefulness for sophisticated reasoning and consistency checking in Knowledge Graphs. In this study, we explore the potential of Large Language Models (LLMs) to enrich ontologies by identifying and asserting class disjointness axioms. Our approach aims at leveraging the implicit knowledge embedded in LLMs, using prompt engineering to elicit this knowledge for classifying ontological disjointness. We validate our methodology on the DBpedia ontology, focusing on open-source LLMs. Our findings suggest that LLMs, when guided by effective prompt strategies, can reliably identify disjoint class relationships, thus streamlining the process of ontology completion without extensive manual input. For comprehensive disjointness enrichment, we propose a process that takes logical relationships between disjointness and subclass statements into account in order to maintain satisfiability and reduce the number of calls to the LLM. This work provides a foundation for future applications of LLMs in automated ontology enhancement and offers insights into optimizing LLM performance through strategic prompt design. Our code is publicly available on GitHub at https://github.com/n28div/llm-disjointness.

The Sticky Path to Expressive Querying: Decidability of Navigational Queries under Existential Rules

Extensive research in the field of ontology-based query answering has led to the identification of numerous fragments of existential rules (also known as tuple-generating dependencies) that exhibit decidable answering of atomic and conjunctive queries. Motivated by the increased theoretical and practical interest in navigational queries, this paper considers the question for which of these fragments decidability of querying extends to regular path queries (RPQs). In fact, decidability of RPQs has recently been shown to generally hold for the comprehensive family of all fragments that come with the guarantee of universal models being reasonably well-shaped (that is, being of finite cliquewidth). Yet, for the second major family of fragments, known as finite unification sets (short: fus), which are based on first-order-rewritability, corresponding results have been largely elusive so far. We complete the picture by showing that RPQ answering over arbitrary fus rulesets is undecidable. On the positive side, we establish that the problem is decidable for the prominent fus subclass of sticky rulesets, with the caveat that a very mild extension of the RPQ formalism turns the problem undecidable again.

Derivation-Graph-Based Characterizations of Decidable Existential Rule Sets

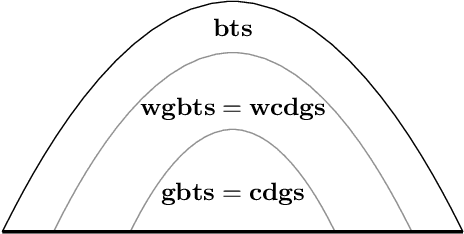
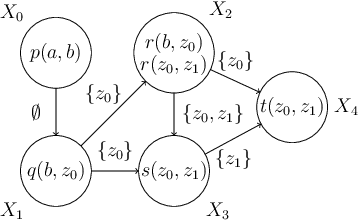
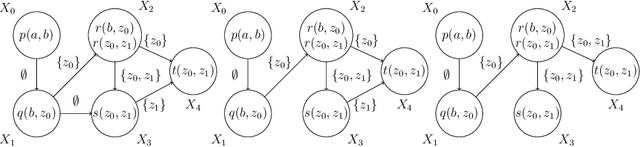
This paper establishes alternative characterizations of very expressive classes of existential rule sets with decidable query entailment. We consider the notable class of greedy bounded-treewidth sets (gbts) and a new, generalized variant, called weakly gbts (wgbts). Revisiting and building on the notion of derivation graphs, we define (weakly) cycle-free derivation graph sets ((w)cdgs) and employ elaborate proof-theoretic arguments to obtain that gbts and cdgs coincide, as do wgbts and wcdgs. These novel characterizations advance our analytic proof-theoretic understanding of existential rules and will likely be instrumental in practice.

Pushing the Boundaries of Tractable Multiperspective Reasoning: A Deduction Calculus for Standpoint EL+

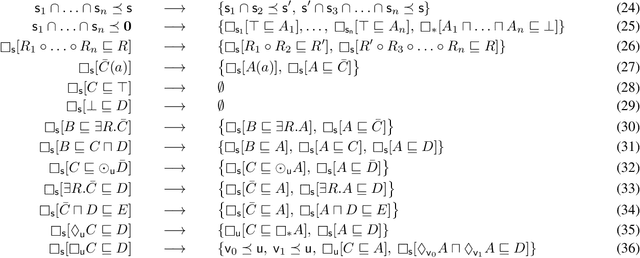
Standpoint EL is a multi-modal extension of the popular description logic EL that allows for the integrated representation of domain knowledge relative to diverse standpoints or perspectives. Advantageously, its satisfiability problem has recently been shown to be in PTime, making it a promising framework for large-scale knowledge integration. In this paper, we show that we can further push the expressivity of this formalism, arriving at an extended logic, called Standpoint EL+, which allows for axiom negation, role chain axioms, self-loops, and other features, while maintaining tractability. This is achieved by designing a satisfiability-checking deduction calculus, which at the same time addresses the need for practical algorithms. We demonstrate the feasibility of our calculus by presenting a prototypical Datalog implementation of its deduction rules.

Decidability of Querying First-Order Theories via Countermodels of Finite Width

We propose a generic framework for establishing the decidability of a wide range of logical entailment problems (briefly called querying), based on the existence of countermodels that are structurally simple, gauged by certain types of width measures (with treewidth and cliquewidth as popular examples). As an important special case of our framework, we identify logics exhibiting width-finite finitely universal model sets, warranting decidable entailment for a wide range of homomorphism-closed queries, subsuming a diverse set of practically relevant query languages. As a particularly powerful width measure, we propose Blumensath's partitionwidth, which subsumes various other commonly considered width measures and exhibits highly favorable computational and structural properties. Focusing on the formalism of existential rules as a popular showcase, we explain how finite partitionwidth sets of rules subsume other known abstract decidable classes but -- leveraging existing notions of stratification -- also cover a wide range of new rulesets. We expose natural limitations for fitting the class of finite unification sets into our picture and provide several options for remedy.

Tractable Diversity: Scalable Multiperspective Ontology Management via Standpoint EL

The tractability of the lightweight description logic EL has allowed for the construction of large and widely used ontologies that support semantic interoperability. However, comprehensive domains with a broad user base are often at odds with strong axiomatisations otherwise useful for inferencing, since these are usually context-dependent and subject to diverging perspectives. In this paper we introduce Standpoint EL, a multi-modal extension of EL that allows for the integrated representation of domain knowledge relative to diverse, possibly conflicting standpoints (or contexts), which can be hierarchically organised and put in relation to each other. We establish that Standpoint EL still exhibits EL's favourable PTime standard reasoning, whereas introducing additional features like empty standpoints, rigid roles, and nominals makes standard reasoning tasks intractable.

Finite-Cliquewidth Sets of Existential Rules: Toward a General Criterion for Decidable yet Highly Expressive Querying

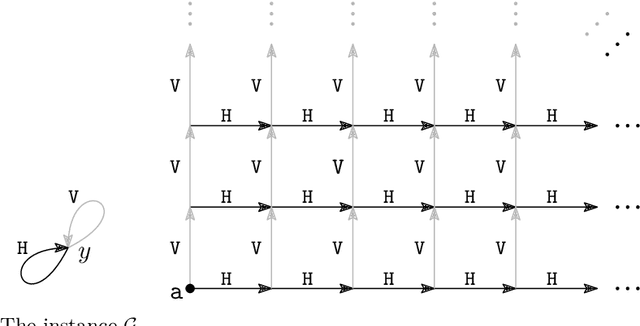
In our pursuit of generic criteria for decidable ontology-based querying, we introduce 'finite-cliquewidth sets' (FCS) of existential rules, a model-theoretically defined class of rule sets, inspired by the cliquewidth measure from graph theory. By a generic argument, we show that FCS ensures decidability of entailment for a sizable class of queries (dubbed 'DaMSOQs') subsuming conjunctive queries (CQs). The FCS class properly generalizes the class of finite-expansion sets (FES), and for signatures of arity at most 2, the class of bounded-treewidth sets (BTS). For higher arities, BTS is only indirectly subsumed by FCS by means of reification. Despite the generality of FCS, we provide a rule set with decidable CQ entailment (by virtue of first-order-rewritability) that falls outside FCS, thus demonstrating the incomparability of FCS and the class of finite-unification sets (FUS). In spite of this, we show that if we restrict ourselves to single-headed rule sets over signatures of arity at most 2, then FCS subsumes FUS.

How to Agree to Disagree: Managing Ontological Perspectives using Standpoint Logic

The importance of taking individual, potentially conflicting perspectives into account when dealing with knowledge has been widely recognised. Many existing ontology management approaches fully merge knowledge perspectives, which may require weakening in order to maintain consistency; others represent the distinct views in an entirely detached way. As an alternative, we propose Standpoint Logic, a simple, yet versatile multi-modal logic ``add-on'' for existing KR languages intended for the integrated representation of domain knowledge relative to diverse, possibly conflicting standpoints, which can be hierarchically organised, combined and put in relation to each other. Starting from the generic framework of First-Order Standpoint Logic (FOSL), we subsequently focus our attention on the fragment of sentential formulas, for which we provide a polytime translation into the standpoint-free version. This result yields decidability and favourable complexities for a variety of highly expressive decidable fragments of first-order logic. Using some elaborate encoding tricks, we then establish a similar translation for the very expressive description logic SROIQb_s underlying the OWL 2 DL ontology language. By virtue of this result, existing highly optimised OWL reasoners can be used to provide practical reasoning support for ontology languages extended by standpoint modelling.