The Sticky Path to Expressive Querying: Decidability of Navigational Queries under Existential Rules

Extensive research in the field of ontology-based query answering has led to the identification of numerous fragments of existential rules (also known as tuple-generating dependencies) that exhibit decidable answering of atomic and conjunctive queries. Motivated by the increased theoretical and practical interest in navigational queries, this paper considers the question for which of these fragments decidability of querying extends to regular path queries (RPQs). In fact, decidability of RPQs has recently been shown to generally hold for the comprehensive family of all fragments that come with the guarantee of universal models being reasonably well-shaped (that is, being of finite cliquewidth). Yet, for the second major family of fragments, known as finite unification sets (short: fus), which are based on first-order-rewritability, corresponding results have been largely elusive so far. We complete the picture by showing that RPQ answering over arbitrary fus rulesets is undecidable. On the positive side, we establish that the problem is decidable for the prominent fus subclass of sticky rulesets, with the caveat that a very mild extension of the RPQ formalism turns the problem undecidable again.

Connecting Proof Theory and Knowledge Representation: Sequent Calculi and the Chase with Existential Rules

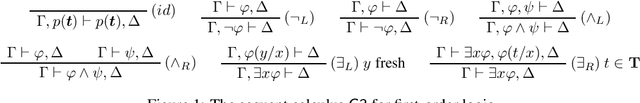
Chase algorithms are indispensable in the domain of knowledge base querying, which enable the extraction of implicit knowledge from a given database via applications of rules from a given ontology. Such algorithms have proved beneficial in identifying logical languages which admit decidable query entailment. Within the discipline of proof theory, sequent calculi have been used to write and design proof-search algorithms to identify decidable classes of logics. In this paper, we show that the chase mechanism in the context of existential rules is in essence the same as proof-search in an extension of Gentzen's sequent calculus for first-order logic. Moreover, we show that proof-search generates universal models of knowledge bases, a feature also exhibited by the chase. Thus, we formally connect a central tool for establishing decidability proof-theoretically with a central decidability tool in the context of knowledge representation.

Decidability of Querying First-Order Theories via Countermodels of Finite Width

We propose a generic framework for establishing the decidability of a wide range of logical entailment problems (briefly called querying), based on the existence of countermodels that are structurally simple, gauged by certain types of width measures (with treewidth and cliquewidth as popular examples). As an important special case of our framework, we identify logics exhibiting width-finite finitely universal model sets, warranting decidable entailment for a wide range of homomorphism-closed queries, subsuming a diverse set of practically relevant query languages. As a particularly powerful width measure, we propose Blumensath's partitionwidth, which subsumes various other commonly considered width measures and exhibits highly favorable computational and structural properties. Focusing on the formalism of existential rules as a popular showcase, we explain how finite partitionwidth sets of rules subsume other known abstract decidable classes but -- leveraging existing notions of stratification -- also cover a wide range of new rulesets. We expose natural limitations for fitting the class of finite unification sets into our picture and provide several options for remedy.

Finite-Cliquewidth Sets of Existential Rules: Toward a General Criterion for Decidable yet Highly Expressive Querying

In our pursuit of generic criteria for decidable ontology-based querying, we introduce 'finite-cliquewidth sets' (FCS) of existential rules, a model-theoretically defined class of rule sets, inspired by the cliquewidth measure from graph theory. By a generic argument, we show that FCS ensures decidability of entailment for a sizable class of queries (dubbed 'DaMSOQs') subsuming conjunctive queries (CQs). The FCS class properly generalizes the class of finite-expansion sets (FES), and for signatures of arity at most 2, the class of bounded-treewidth sets (BTS). For higher arities, BTS is only indirectly subsumed by FCS by means of reification. Despite the generality of FCS, we provide a rule set with decidable CQ entailment (by virtue of first-order-rewritability) that falls outside FCS, thus demonstrating the incomparability of FCS and the class of finite-unification sets (FUS). In spite of this, we show that if we restrict ourselves to single-headed rule sets over signatures of arity at most 2, then FCS subsumes FUS.