Connecting Proof Theory and Knowledge Representation: Sequent Calculi and the Chase with Existential Rules
Paper and Code
Jun 05, 2023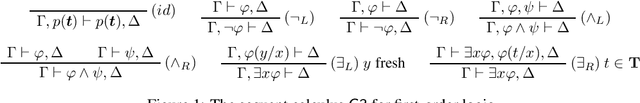


Chase algorithms are indispensable in the domain of knowledge base querying, which enable the extraction of implicit knowledge from a given database via applications of rules from a given ontology. Such algorithms have proved beneficial in identifying logical languages which admit decidable query entailment. Within the discipline of proof theory, sequent calculi have been used to write and design proof-search algorithms to identify decidable classes of logics. In this paper, we show that the chase mechanism in the context of existential rules is in essence the same as proof-search in an extension of Gentzen's sequent calculus for first-order logic. Moreover, we show that proof-search generates universal models of knowledge bases, a feature also exhibited by the chase. Thus, we formally connect a central tool for establishing decidability proof-theoretically with a central decidability tool in the context of knowledge representation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge