Constructive Interpolation and Concept-Based Beth Definability for Description Logics via Sequents

We introduce a constructive method applicable to a large number of description logics (DLs) for establishing the concept-based Beth definability property (CBP) based on sequent systems. Using the highly expressive DL RIQ as a case study, we introduce novel sequent calculi for RIQ-ontologies and show how certain interpolants can be computed from sequent calculus proofs, which permit the extraction of explicit definitions of implicitly definable concepts. To the best of our knowledge, this is the first sequent-based approach to computing interpolants and definitions within the context of DLs, as well as the first proof that RIQ enjoys the CBP. Moreover, due to the modularity of our sequent systems, our results hold for any restriction of RIQ, and are applicable to other DLs by suitable modifications.

Derivation-Graph-Based Characterizations of Decidable Existential Rule Sets

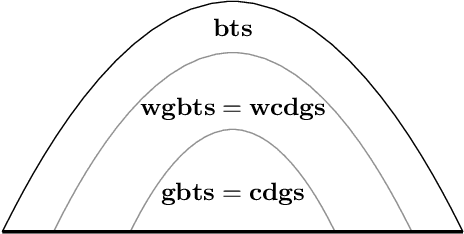
This paper establishes alternative characterizations of very expressive classes of existential rule sets with decidable query entailment. We consider the notable class of greedy bounded-treewidth sets (gbts) and a new, generalized variant, called weakly gbts (wgbts). Revisiting and building on the notion of derivation graphs, we define (weakly) cycle-free derivation graph sets ((w)cdgs) and employ elaborate proof-theoretic arguments to obtain that gbts and cdgs coincide, as do wgbts and wcdgs. These novel characterizations advance our analytic proof-theoretic understanding of existential rules and will likely be instrumental in practice.

Connecting Proof Theory and Knowledge Representation: Sequent Calculi and the Chase with Existential Rules

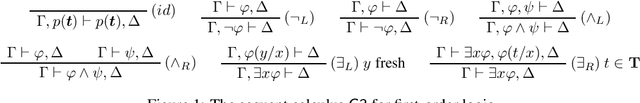
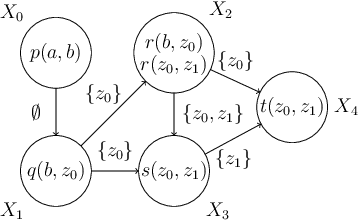
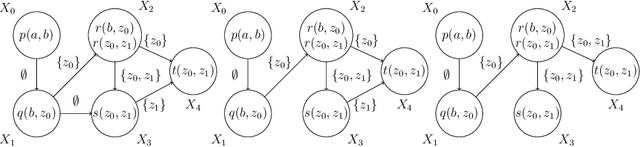
Chase algorithms are indispensable in the domain of knowledge base querying, which enable the extraction of implicit knowledge from a given database via applications of rules from a given ontology. Such algorithms have proved beneficial in identifying logical languages which admit decidable query entailment. Within the discipline of proof theory, sequent calculi have been used to write and design proof-search algorithms to identify decidable classes of logics. In this paper, we show that the chase mechanism in the context of existential rules is in essence the same as proof-search in an extension of Gentzen's sequent calculus for first-order logic. Moreover, we show that proof-search generates universal models of knowledge bases, a feature also exhibited by the chase. Thus, we formally connect a central tool for establishing decidability proof-theoretically with a central decidability tool in the context of knowledge representation.

Standpoint Linear Temporal Logic

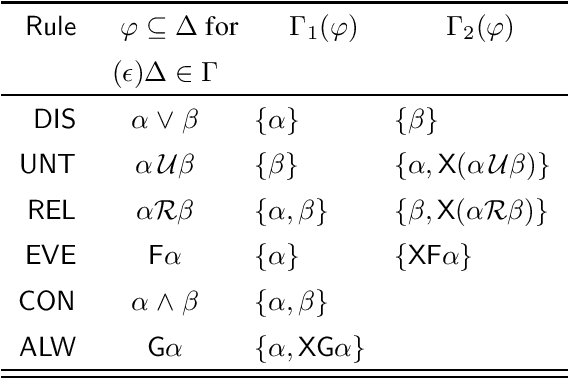
Many complex scenarios require the coordination of agents possessing unique points of view and distinct semantic commitments. In response, standpoint logic (SL) was introduced in the context of knowledge integration, allowing one to reason with diverse and potentially conflicting viewpoints by means of indexed modalities. Another multi-modal logic of import is linear temporal logic (LTL) - a formalism used to express temporal properties of systems and processes, having prominence in formal methods and fields related to artificial intelligence. In this paper, we present standpoint linear temporal logic (SLTL), a new logic that combines the temporal features of LTL with the multi-perspective modelling capacity of SL. We define the logic SLTL, its syntax, and its semantics, establish its decidability and complexity, and provide a terminating tableau calculus to automate SLTL reasoning. Conveniently, this offers a clear path to extend existing LTL reasoners with practical reasoning support for temporal reasoning in multi-perspective settings.

Decidability of Querying First-Order Theories via Countermodels of Finite Width

We propose a generic framework for establishing the decidability of a wide range of logical entailment problems (briefly called querying), based on the existence of countermodels that are structurally simple, gauged by certain types of width measures (with treewidth and cliquewidth as popular examples). As an important special case of our framework, we identify logics exhibiting width-finite finitely universal model sets, warranting decidable entailment for a wide range of homomorphism-closed queries, subsuming a diverse set of practically relevant query languages. As a particularly powerful width measure, we propose Blumensath's partitionwidth, which subsumes various other commonly considered width measures and exhibits highly favorable computational and structural properties. Focusing on the formalism of existential rules as a popular showcase, we explain how finite partitionwidth sets of rules subsume other known abstract decidable classes but -- leveraging existing notions of stratification -- also cover a wide range of new rulesets. We expose natural limitations for fitting the class of finite unification sets into our picture and provide several options for remedy.

Finite-Cliquewidth Sets of Existential Rules: Toward a General Criterion for Decidable yet Highly Expressive Querying

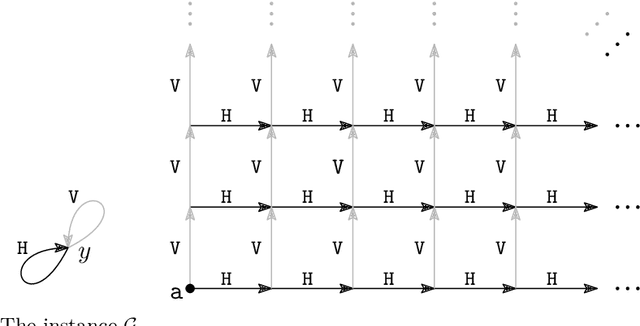
In our pursuit of generic criteria for decidable ontology-based querying, we introduce 'finite-cliquewidth sets' (FCS) of existential rules, a model-theoretically defined class of rule sets, inspired by the cliquewidth measure from graph theory. By a generic argument, we show that FCS ensures decidability of entailment for a sizable class of queries (dubbed 'DaMSOQs') subsuming conjunctive queries (CQs). The FCS class properly generalizes the class of finite-expansion sets (FES), and for signatures of arity at most 2, the class of bounded-treewidth sets (BTS). For higher arities, BTS is only indirectly subsumed by FCS by means of reification. Despite the generality of FCS, we provide a rule set with decidable CQ entailment (by virtue of first-order-rewritability) that falls outside FCS, thus demonstrating the incomparability of FCS and the class of finite-unification sets (FUS). In spite of this, we show that if we restrict ourselves to single-headed rule sets over signatures of arity at most 2, then FCS subsumes FUS.

Automating Reasoning with Standpoint Logic via Nested Sequents

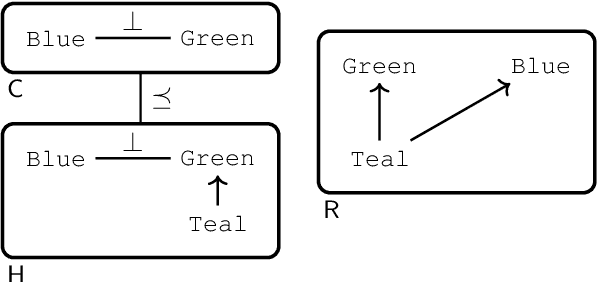
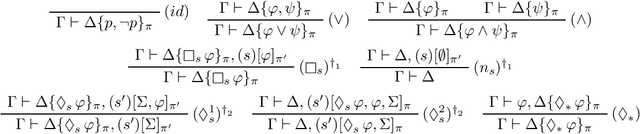
Standpoint logic is a recently proposed formalism in the context of knowledge integration, which advocates a multi-perspective approach permitting reasoning with a selection of diverse and possibly conflicting standpoints rather than forcing their unification. In this paper, we introduce nested sequent calculi for propositional standpoint logics--proof systems that manipulate trees whose nodes are multisets of formulae--and show how to automate standpoint reasoning by means of non-deterministic proof-search algorithms. To obtain worst-case complexity-optimal proof-search, we introduce a novel technique in the context of nested sequents, referred to as "coloring," which consists of taking a formula as input, guessing a certain coloring of its subformulae, and then running proof-search in a nested sequent calculus on the colored input. Our technique lets us decide the validity of standpoint formulae in CoNP since proof-search only produces a partial proof relative to each permitted coloring of the input. We show how all partial proofs can be fused together to construct a complete proof when the input is valid, and how certain partial proofs can be transformed into a counter-model when the input is invalid. These "certificates" (i.e. proofs and counter-models) serve as explanations of the (in)validity of the input.