Counterfactual Scenarios for Automated Planning

Counterfactual Explanations (CEs) are a powerful technique used to explain Machine Learning models by showing how the input to a model should be minimally changed for the model to produce a different output. Similar proposals have been made in the context of Automated Planning, where CEs have been characterised in terms of minimal modifications to an existing plan that would result in the satisfaction of a different goal. While such explanations may help diagnose faults and reason about the characteristics of a plan, they fail to capture higher-level properties of the problem being solved. To address this limitation, we propose a novel explanation paradigm that is based on counterfactual scenarios. In particular, given a planning problem $P$ and an \ltlf formula $\psi$ defining desired properties of a plan, counterfactual scenarios identify minimal modifications to $P$ such that it admits plans that comply with $\psi$. In this paper, we present two qualitative instantiations of counterfactual scenarios based on an explicit quantification over plans that must satisfy $\psi$. We then characterise the computational complexity of generating such counterfactual scenarios when different types of changes are allowed on $P$. We show that producing counterfactual scenarios is often only as expensive as computing a plan for $P$, thus demonstrating the practical viability of our proposal and ultimately providing a framework to construct practical algorithms in this area.

Decidable Fragments of LTLf Modulo Theories (Extended Version)

We study Linear Temporal Logic Modulo Theories over Finite Traces (LTLfMT), a recently introduced extension of LTL over finite traces (LTLf) where propositions are replaced by first-order formulas and where first-order variables referring to different time points can be compared. In general, LTLfMT was shown to be semi-decidable for any decidable first-order theory (e.g., linear arithmetics), with a tableau-based semi-decision procedure. In this paper we present a sound and complete pruning rule for the LTLfMT tableau. We show that for any LTLfMT formula that satisfies an abstract, semantic condition, that we call finite memory, the tableau augmented with the new rule is also guaranteed to terminate. Last but not least, this technique allows us to establish novel decidability results for the satisfiability of several fragments of LTLfMT, as well as to give new decidability proofs for classes that are already known.

Controller Synthesis for Timeline-based Games

In the timeline-based approach to planning, the evolution over time of a set of state variables (the timelines) is governed by a set of temporal constraints. Traditional timeline-based planning systems excel at the integration of planning with execution by handling temporal uncertainty. In order to handle general nondeterminism as well, the concept of timeline-based games has been recently introduced. It has been proved that finding whether a winning strategy exists for such games is 2EXPTIME-complete. However, a concrete approach to synthesize controllers implementing such strategies is missing. This paper fills this gap, by providing an effective and computationally optimal approach to controller synthesis for timeline-based games.

Standpoint Linear Temporal Logic

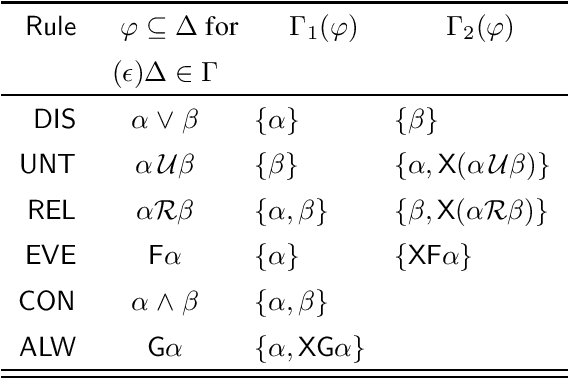
Many complex scenarios require the coordination of agents possessing unique points of view and distinct semantic commitments. In response, standpoint logic (SL) was introduced in the context of knowledge integration, allowing one to reason with diverse and potentially conflicting viewpoints by means of indexed modalities. Another multi-modal logic of import is linear temporal logic (LTL) - a formalism used to express temporal properties of systems and processes, having prominence in formal methods and fields related to artificial intelligence. In this paper, we present standpoint linear temporal logic (SLTL), a new logic that combines the temporal features of LTL with the multi-perspective modelling capacity of SL. We define the logic SLTL, its syntax, and its semantics, establish its decidability and complexity, and provide a terminating tableau calculus to automate SLTL reasoning. Conveniently, this offers a clear path to extend existing LTL reasoners with practical reasoning support for temporal reasoning in multi-perspective settings.

A first-order logic characterization of safety and co-safety languages

Linear Temporal Logic (LTL) is one of the most popular temporal logics, that comes into play in a variety of branches of computer science. Among the various reasons of its widespread use there are its strong foundational properties: LTL is equivalent to counter-free omega-automata, to star-free omega-regular expressions, and (by Kamp's theorem) to the first-order theory of one successor (S1S[FO]). Safety and co-safety languages, where a finite prefix suffices to establish whether a word does not belong or belongs to the language, respectively, play a crucial role in lowering the complexity of problems like model checking and reactive synthesis for LTL. SafetyLTL (resp., coSafetyLTL) is a fragment of LTL where only universal (resp., existential) temporal modalities are allowed, that recognises safety (resp., co-safety) languages only. The main contribution of this paper is the introduction of a fragment of S1S[FO], called SafetyFO, and of its dual coSafetyFO, which are expressively complete with respect to the LTL-definable safety and co-safety languages. We prove that they exactly characterize SafetyLTL and coSafetyLTL, respectively, a result that joins Kamp's theorem, and provides a clearer view of the characterization of (fragments of) LTL in terms of first-order languages. In addition, it gives a direct, compact, and self-contained proof that any safety language definable in LTL is definable in SafetyLTL as well. As a by-product, we obtain some interesting results on the expressive power of the weak tomorrow operator of SafetyLTL, interpreted over finite and infinite words. Moreover, we prove that, when interpreted over finite words, SafetyLTL (resp. coSafetyLTL) devoid of the tomorrow (resp., weak tomorrow) operator captures the safety (resp., co-safety) fragment of LTL over finite words.

Linear Temporal Logic Modulo Theories over Finite Traces (Extended Version)

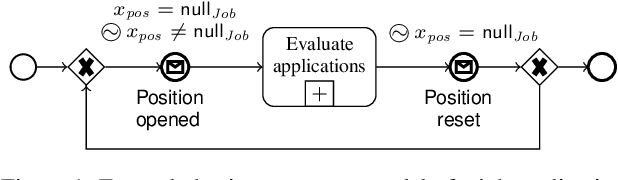
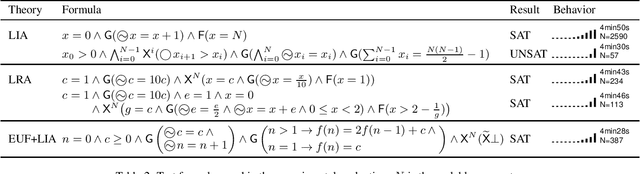
This paper studies Linear Temporal Logic over Finite Traces (LTLf) where proposition letters are replaced with first-order formulas interpreted over arbitrary theories, in the spirit of Satisfiability Modulo Theories. The resulting logic, called LTLf Modulo Theories (LTLfMT), is semi-decidable. Nevertheless, its high expressiveness comes useful in a number of use cases, such as model-checking of data-aware processes and data-aware planning. Despite the general undecidability of these problems, being able to solve satisfiable instances is a compromise worth studying. After motivating and describing such use cases, we provide a sound and complete semi-decision procedure for LTLfMT based on the SMT encoding of a one-pass tree-shaped tableau system. The algorithm is implemented in the BLACK satisfiability checking tool, and an experimental evaluation shows the feasibility of the approach on novel benchmarks.

Timeline-based planning: Expressiveness and Complexity

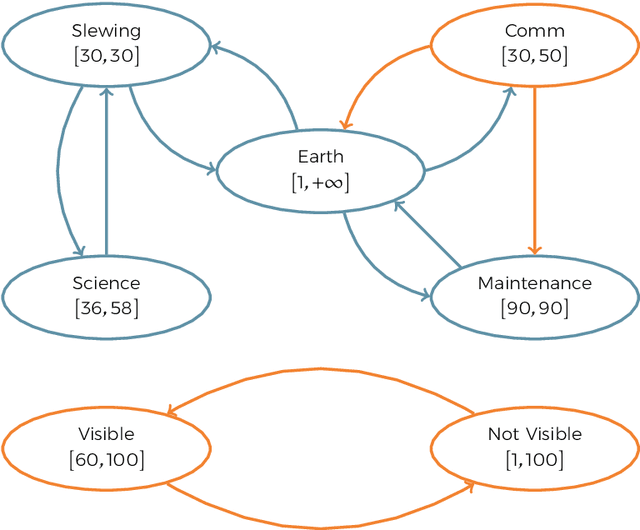
Timeline-based planning is an approach originally developed in the context of space mission planning and scheduling, where problem domains are modelled as systems made of a number of independent but interacting components, whose behaviour over time, the timelines, is governed by a set of temporal constraints. This approach is different from the action-based perspective of common PDDL-like planning languages. Timeline-based systems have been successfully deployed in a number of space missions and other domains. However, despite this practical success, a thorough theoretical understanding of the paradigm was missing. This thesis fills this gap, providing the first detailed account of formal and computational properties of the timeline-based approach to planning. In particular, we show that a particularly restricted variant of the formalism is already expressive enough to compactly capture action-based temporal planning problems. Then, finding a solution plan for a timeline-based planning problem is proved to be EXPSPACE-complete. Then, we study the problem of timeline-based planning with uncertainty, that include external components whose behaviour is not under the control of the planned system. We identify a few issues in the state-of-the-art approach based on flexible plans, proposing timeline-based games, a more general game-theoretic formulation of the problem, that addresses those issues. We show that winning strategies for such games can be found in doubly-exponential time. Then, we study the expressiveness of the formalism from a logic point of view, showing that (most of) timeline-based planning problems can be captured by Bounded TPTL with Past, a fragment of TPTL+P that, unlike the latter, keeps an EXPSPACE satisfiability problem. The logic is introduced and its satisfiabilty problem is solved by extending a recent one-pass tree-shaped tableau method for LTL.

A game-theoretic approach to timeline-based planning with uncertainty

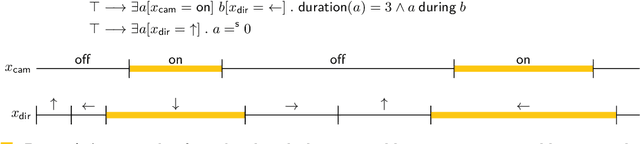
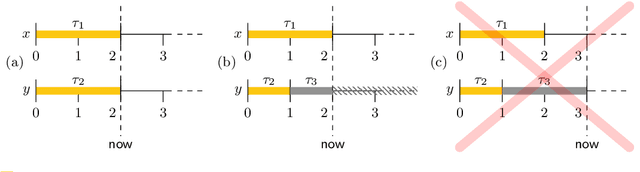
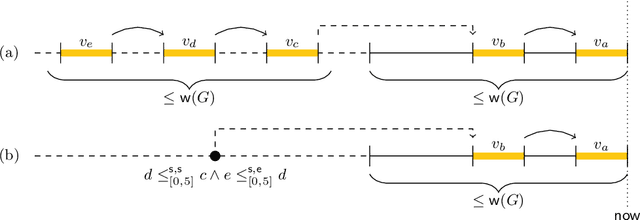
In timeline-based planning, domains are described as sets of independent, but interacting, components, whose behaviour over time (the set of timelines) is governed by a set of temporal constraints. A distinguishing feature of timeline-based planning systems is the ability to integrate planning with execution by synthesising control strategies for flexible plans. However, flexible plans can only represent temporal uncertainty, while more complex forms of nondeterminism are needed to deal with a wider range of realistic problems. In this paper, we propose a novel game-theoretic approach to timeline-based planning problems, generalising the state of the art while uniformly handling temporal uncertainty and nondeterminism. We define a general concept of timeline-based game and we show that the notion of winning strategy for these games is strictly more general than that of control strategy for dynamically controllable flexible plans. Moreover, we show that the problem of establishing the existence of such winning strategies is decidable using a doubly exponential amount of space.