Optimal task and motion planning and execution for human-robot multi-agent systems in dynamic environments

Combining symbolic and geometric reasoning in multi-agent systems is a challenging task that involves planning, scheduling, and synchronization problems. Existing works overlooked the variability of task duration and geometric feasibility that is intrinsic to these systems because of the interaction between agents and the environment. We propose a combined task and motion planning approach to optimize sequencing, assignment, and execution of tasks under temporal and spatial variability. The framework relies on decoupling tasks and actions, where an action is one possible geometric realization of a symbolic task. At the task level, timeline-based planning deals with temporal constraints, duration variability, and synergic assignment of tasks. At the action level, online motion planning plans for the actual movements dealing with environmental changes. We demonstrate the approach effectiveness in a collaborative manufacturing scenario, in which a robotic arm and a human worker shall assemble a mosaic in the shortest time possible. Compared with existing works, our approach applies to a broader range of applications and reduces the execution time of the process.

A game-theoretic approach to timeline-based planning with uncertainty

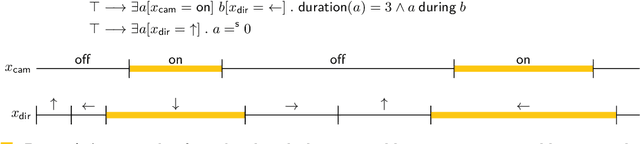
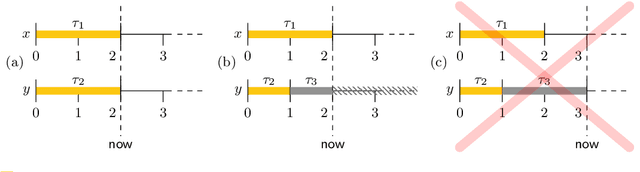
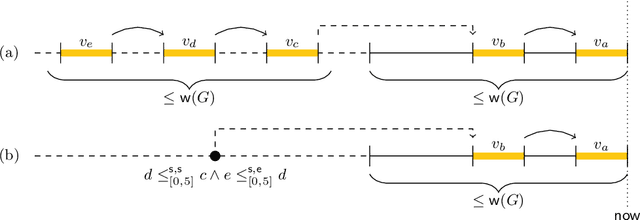
In timeline-based planning, domains are described as sets of independent, but interacting, components, whose behaviour over time (the set of timelines) is governed by a set of temporal constraints. A distinguishing feature of timeline-based planning systems is the ability to integrate planning with execution by synthesising control strategies for flexible plans. However, flexible plans can only represent temporal uncertainty, while more complex forms of nondeterminism are needed to deal with a wider range of realistic problems. In this paper, we propose a novel game-theoretic approach to timeline-based planning problems, generalising the state of the art while uniformly handling temporal uncertainty and nondeterminism. We define a general concept of timeline-based game and we show that the notion of winning strategy for these games is strictly more general than that of control strategy for dynamically controllable flexible plans. Moreover, we show that the problem of establishing the existence of such winning strategies is decidable using a doubly exponential amount of space.