Marta Cialdea Mayer
Option Discovery for Autonomous Generation of Symbolic Knowledge
Jun 03, 2022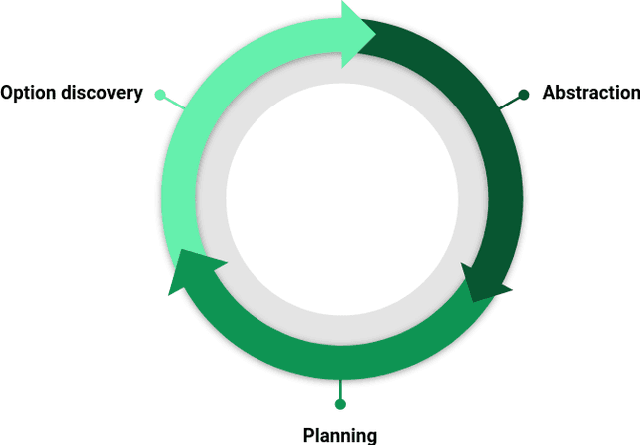
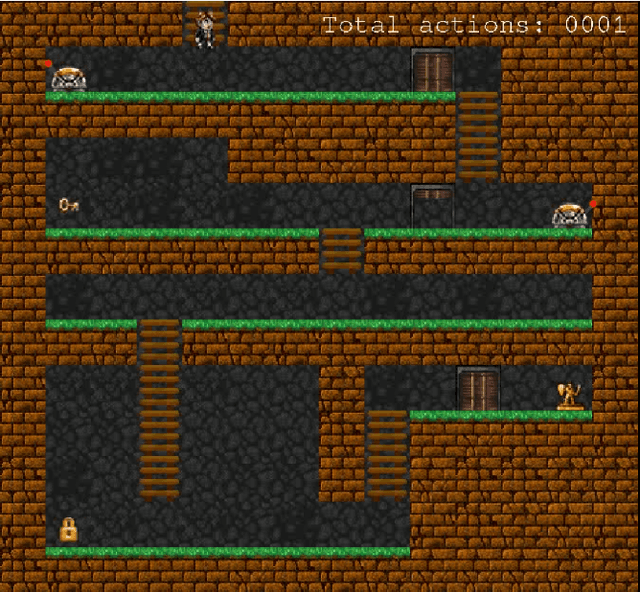


Abstract:In this work we present an empirical study where we demonstrate the possibility of developing an artificial agent that is capable to autonomously explore an experimental scenario. During the exploration, the agent is able to discover and learn interesting options allowing to interact with the environment without any pre-assigned goal, then abstract and re-use the acquired knowledge to solve possible tasks assigned ex-post. We test the system in the so-called Treasure Game domain described in the recent literature and we empirically demonstrate that the discovered options can be abstracted in an probabilistic symbolic planning model (using the PPDDL language), which allowed the agent to generate symbolic plans to achieve extrinsic goals.
A game-theoretic approach to timeline-based planning with uncertainty
Jul 12, 2018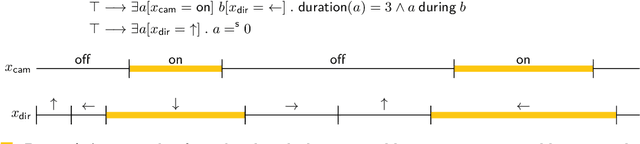
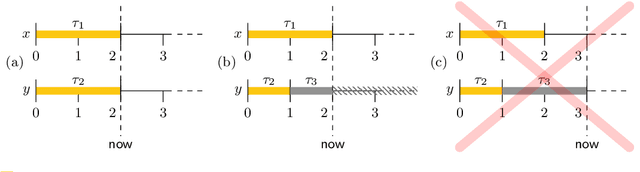
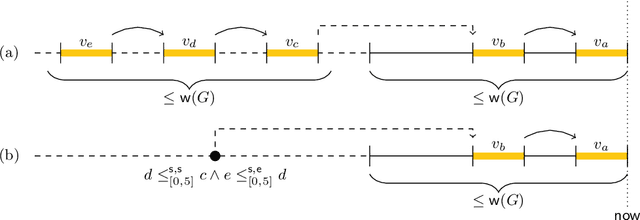
Abstract:In timeline-based planning, domains are described as sets of independent, but interacting, components, whose behaviour over time (the set of timelines) is governed by a set of temporal constraints. A distinguishing feature of timeline-based planning systems is the ability to integrate planning with execution by synthesising control strategies for flexible plans. However, flexible plans can only represent temporal uncertainty, while more complex forms of nondeterminism are needed to deal with a wider range of realistic problems. In this paper, we propose a novel game-theoretic approach to timeline-based planning problems, generalising the state of the art while uniformly handling temporal uncertainty and nondeterminism. We define a general concept of timeline-based game and we show that the notion of winning strategy for these games is strictly more general than that of control strategy for dynamically controllable flexible plans. Moreover, we show that the problem of establishing the existence of such winning strategies is decidable using a doubly exponential amount of space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge