A first-order logic characterization of safety and co-safety languages

Linear Temporal Logic (LTL) is one of the most popular temporal logics, that comes into play in a variety of branches of computer science. Among the various reasons of its widespread use there are its strong foundational properties: LTL is equivalent to counter-free omega-automata, to star-free omega-regular expressions, and (by Kamp's theorem) to the first-order theory of one successor (S1S[FO]). Safety and co-safety languages, where a finite prefix suffices to establish whether a word does not belong or belongs to the language, respectively, play a crucial role in lowering the complexity of problems like model checking and reactive synthesis for LTL. SafetyLTL (resp., coSafetyLTL) is a fragment of LTL where only universal (resp., existential) temporal modalities are allowed, that recognises safety (resp., co-safety) languages only. The main contribution of this paper is the introduction of a fragment of S1S[FO], called SafetyFO, and of its dual coSafetyFO, which are expressively complete with respect to the LTL-definable safety and co-safety languages. We prove that they exactly characterize SafetyLTL and coSafetyLTL, respectively, a result that joins Kamp's theorem, and provides a clearer view of the characterization of (fragments of) LTL in terms of first-order languages. In addition, it gives a direct, compact, and self-contained proof that any safety language definable in LTL is definable in SafetyLTL as well. As a by-product, we obtain some interesting results on the expressive power of the weak tomorrow operator of SafetyLTL, interpreted over finite and infinite words. Moreover, we prove that, when interpreted over finite words, SafetyLTL (resp. coSafetyLTL) devoid of the tomorrow (resp., weak tomorrow) operator captures the safety (resp., co-safety) fragment of LTL over finite words.

Towards Efficient Anytime Computation and Execution of Decoupled Robustness Envelopes for Temporal Plans

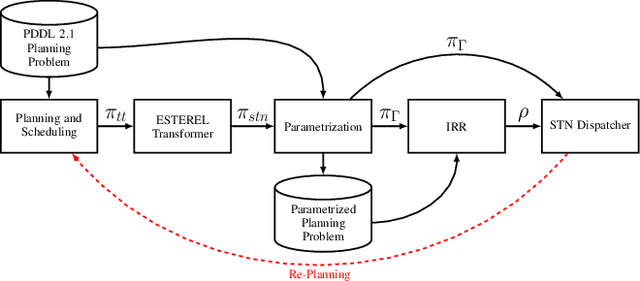
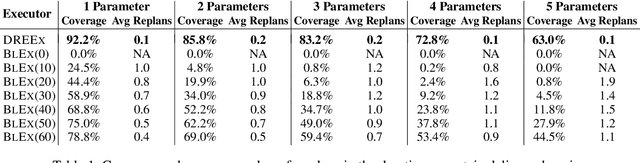
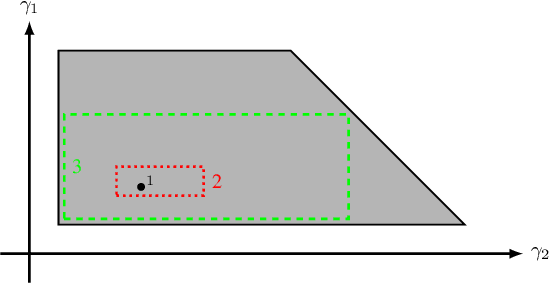
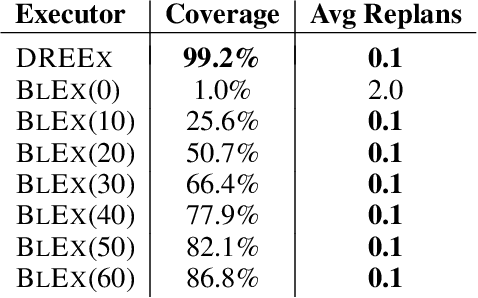
One of the major limitations for the employment of model-based planning and scheduling in practical applications is the need of costly re-planning when an incongruence between the observed reality and the formal model is encountered during execution. Robustness Envelopes characterize the set of possible contingencies that a plan is able to address without re-planning, but their exact computation is extremely expensive; furthermore, general robustness envelopes are not amenable for efficient execution. In this paper, we present a novel, anytime algorithm to approximate Robustness Envelopes, making them scalable and executable. This is proven by an experimental analysis showing the efficiency of the algorithm, and by a concrete case study where the execution of robustness envelopes significantly reduces the number of re-plannings.

Temporal Planning with Intermediate Conditions and Effects

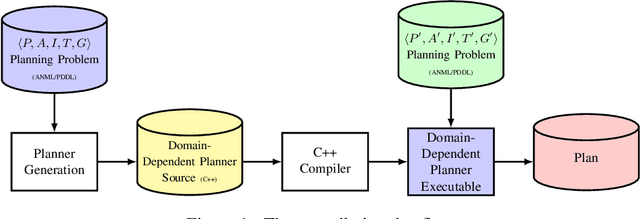
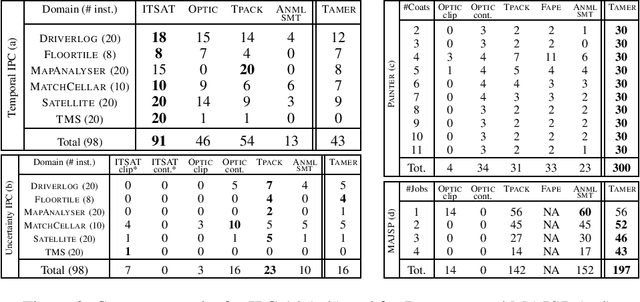
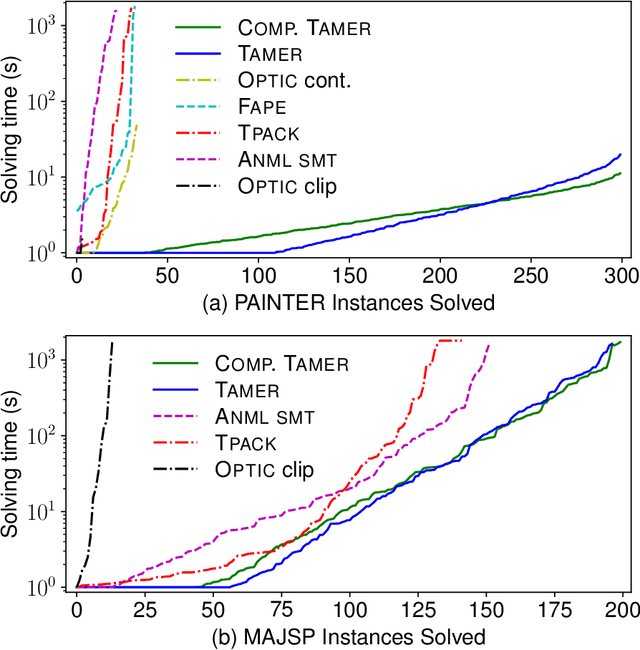
Automated temporal planning is the technology of choice when controlling systems that can execute more actions in parallel and when temporal constraints, such as deadlines, are needed in the model. One limitation of several action-based planning systems is that actions are modeled as intervals having conditions and effects only at the extremes and as invariants, but no conditions nor effects can be specified at arbitrary points or sub-intervals. In this paper, we address this limitation by providing an effective heuristic-search technique for temporal planning, allowing the definition of actions with conditions and effects at any arbitrary time within the action duration. We experimentally demonstrate that our approach is far better than standard encodings in PDDL 2.1 and is competitive with other approaches that can (directly or indirectly) represent intermediate action conditions or effects.

Computing Small Unsatisfiable Cores in Satisfiability Modulo Theories

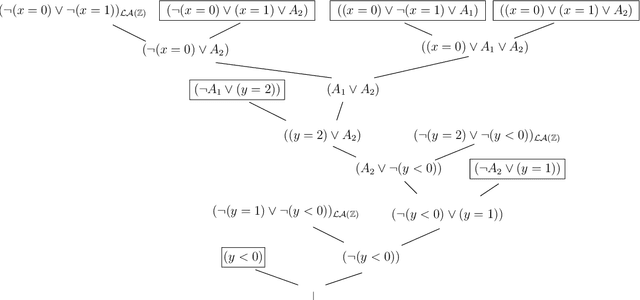
The problem of finding small unsatisfiable cores for SAT formulas has recently received a lot of interest, mostly for its applications in formal verification. However, propositional logic is often not expressive enough for representing many interesting verification problems, which can be more naturally addressed in the framework of Satisfiability Modulo Theories, SMT. Surprisingly, the problem of finding unsatisfiable cores in SMT has received very little attention in the literature. In this paper we present a novel approach to this problem, called the Lemma-Lifting approach. The main idea is to combine an SMT solver with an external propositional core extractor. The SMT solver produces the theory lemmas found during the search, dynamically lifting the suitable amount of theory information to the Boolean level. The core extractor is then called on the Boolean abstraction of the original SMT problem and of the theory lemmas. This results in an unsatisfiable core for the original SMT problem, once the remaining theory lemmas are removed. The approach is conceptually interesting, and has several advantages in practice. In fact, it is extremely simple to implement and to update, and it can be interfaced with every propositional core extractor in a plug-and-play manner, so as to benefit for free of all unsat-core reduction techniques which have been or will be made available. We have evaluated our algorithm with a very extensive empirical test on SMT-LIB benchmarks, which confirms the validity and potential of this approach.