Exploiting Symbolic Heuristics for the Synthesis of Domain-Specific Temporal Planning Guidance using Reinforcement Learning

Recent work investigated the use of Reinforcement Learning (RL) for the synthesis of heuristic guidance to improve the performance of temporal planners when a domain is fixed and a set of training problems (not plans) is given. The idea is to extract a heuristic from the value function of a particular (possibly infinite-state) MDP constructed over the training problems. In this paper, we propose an evolution of this learning and planning framework that focuses on exploiting the information provided by symbolic heuristics during both the RL and planning phases. First, we formalize different reward schemata for the synthesis and use symbolic heuristics to mitigate the problems caused by the truncation of episodes needed to deal with the potentially infinite MDP. Second, we propose learning a residual of an existing symbolic heuristic, which is a "correction" of the heuristic value, instead of eagerly learning the whole heuristic from scratch. Finally, we use the learned heuristic in combination with a symbolic heuristic using a multiple-queue planning approach to balance systematic search with imperfect learned information. We experimentally compare all the approaches, highlighting their strengths and weaknesses and significantly advancing the state of the art for this planning and learning schema.

A Meta-Engine Framework for Interleaved Task and Motion Planning using Topological Refinements

Task And Motion Planning (TAMP) is the problem of finding a solution to an automated planning problem that includes discrete actions executable by low-level continuous motions. This field is gaining increasing interest within the robotics community, as it significantly enhances robot's autonomy in real-world applications. Many solutions and formulations exist, but no clear standard representation has emerged. In this paper, we propose a general and open-source framework for modeling and benchmarking TAMP problems. Moreover, we introduce an innovative meta-technique to solve TAMP problems involving moving agents and multiple task-state-dependent obstacles. This approach enables using any off-the-shelf task planner and motion planner while leveraging a geometric analysis of the motion planner's search space to prune the task planner's exploration, enhancing its efficiency. We also show how to specialize this meta-engine for the case of an incremental SMT-based planner. We demonstrate the effectiveness of our approach across benchmark problems of increasing complexity, where robots must navigate environments with movable obstacles. Finally, we integrate state-of-the-art TAMP algorithms into our framework and compare their performance with our achievements.

Temporal Planning with Intermediate Conditions and Effects

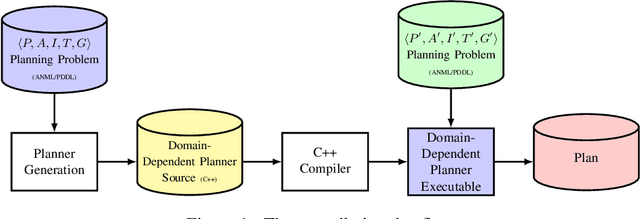
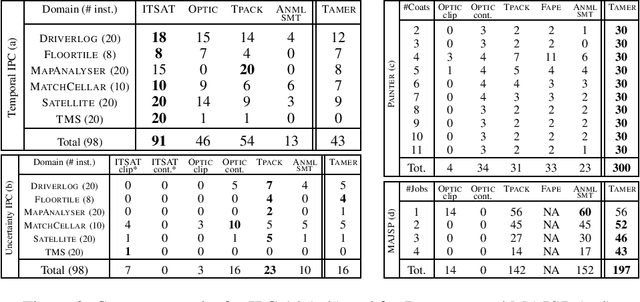
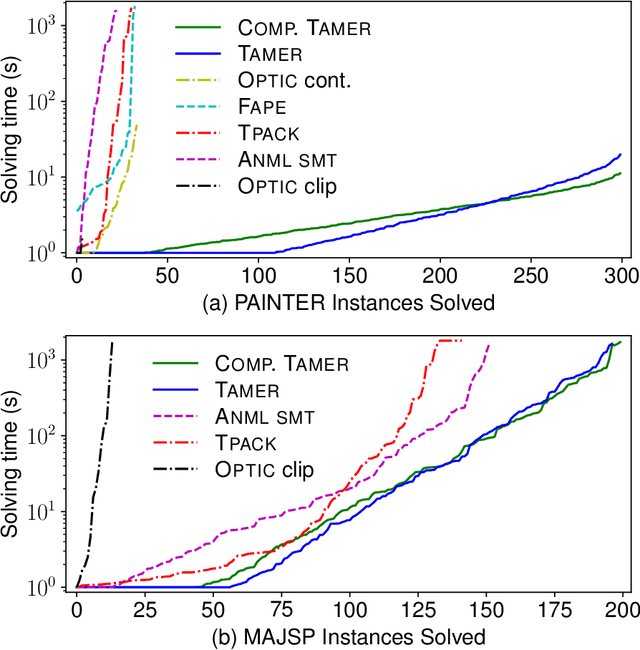
Automated temporal planning is the technology of choice when controlling systems that can execute more actions in parallel and when temporal constraints, such as deadlines, are needed in the model. One limitation of several action-based planning systems is that actions are modeled as intervals having conditions and effects only at the extremes and as invariants, but no conditions nor effects can be specified at arbitrary points or sub-intervals. In this paper, we address this limitation by providing an effective heuristic-search technique for temporal planning, allowing the definition of actions with conditions and effects at any arbitrary time within the action duration. We experimentally demonstrate that our approach is far better than standard encodings in PDDL 2.1 and is competitive with other approaches that can (directly or indirectly) represent intermediate action conditions or effects.