Derivation-Graph-Based Characterizations of Decidable Existential Rule Sets
Paper and Code
Jul 18, 2023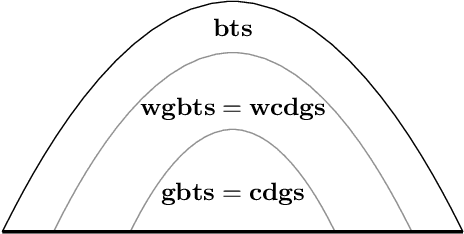
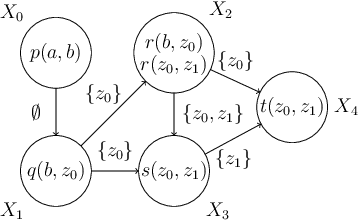
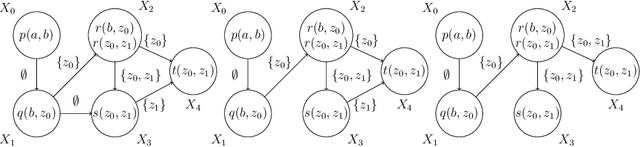
This paper establishes alternative characterizations of very expressive classes of existential rule sets with decidable query entailment. We consider the notable class of greedy bounded-treewidth sets (gbts) and a new, generalized variant, called weakly gbts (wgbts). Revisiting and building on the notion of derivation graphs, we define (weakly) cycle-free derivation graph sets ((w)cdgs) and employ elaborate proof-theoretic arguments to obtain that gbts and cdgs coincide, as do wgbts and wcdgs. These novel characterizations advance our analytic proof-theoretic understanding of existential rules and will likely be instrumental in practice.
* accepted to JELIA 2023
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge