Combining Existential Rules and Transitivity: Next Steps

We consider existential rules (aka Datalog+) as a formalism for specifying ontologies. In recent years, many classes of existential rules have been exhibited for which conjunctive query (CQ) entailment is decidable. However, most of these classes cannot express transitivity of binary relations, a frequently used modelling construct. In this paper, we address the issue of whether transitivity can be safely combined with decidable classes of existential rules. First, we prove that transitivity is incompatible with one of the simplest decidable classes, namely aGRD (acyclic graph of rule dependencies), which clarifies the landscape of `finite expansion sets' of rules. Second, we show that transitivity can be safely added to linear rules (a subclass of guarded rules, which generalizes the description logic DL-Lite-R) in the case of atomic CQs, and also for general CQs if we place a minor syntactic restriction on the rule set. This is shown by means of a novel query rewriting algorithm that is specially tailored to handle transitivity rules. Third, for the identified decidable cases, we pinpoint the combined and data complexities of query entailment.

A General Modifier-based Framework for Inconsistency-Tolerant Query Answering

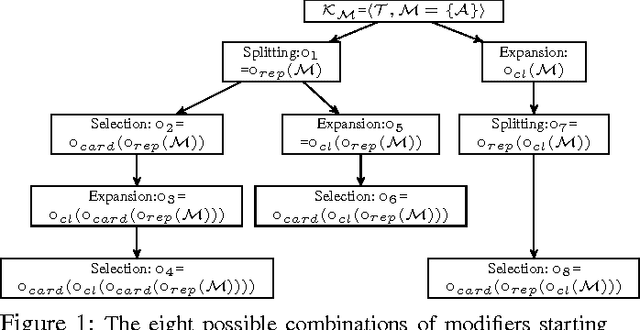
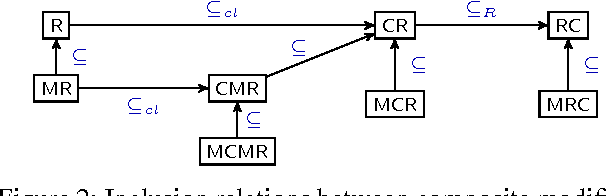
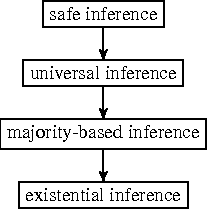
We propose a general framework for inconsistency-tolerant query answering within existential rule setting. This framework unifies the main semantics proposed by the state of art and introduces new ones based on cardinality and majority principles. It relies on two key notions: modifiers and inference strategies. An inconsistency-tolerant semantics is seen as a composite modifier plus an inference strategy. We compare the obtained semantics from a productivity point of view.

Extending Acyclicity Notions for Existential Rules (\emph{long version})

Existential rules have been proposed for representing ontological knowledge, specifically in the context of Ontology-Based Query Answering. Entailment with existential rules is undecidable. We focus in this paper on conditions that ensure the termination of a breadth-first forward chaining algorithm known as the chase. First, we propose a new tool that allows to extend existing acyclicity conditions ensuring chase termination, while keeping good complexity properties. Second, we consider the extension to existential rules with nonmonotonic negation under stable model semantics and further extend acyclicity results obtained in the positive case.

Revisiting Chase Termination for Existential Rules and their Extension to Nonmonotonic Negation

Existential rules have been proposed for representing ontological knowledge, specifically in the context of Ontology- Based Data Access. Entailment with existential rules is undecidable. We focus in this paper on conditions that ensure the termination of a breadth-first forward chaining algorithm known as the chase. Several variants of the chase have been proposed. In the first part of this paper, we propose a new tool that allows to extend existing acyclicity conditions ensuring chase termination, while keeping good complexity properties. In the second part, we study the extension to existential rules with nonmonotonic negation under stable model semantics, discuss the relevancy of the chase variants for these rules and further extend acyclicity results obtained in the positive case.