Preference Reasoning in Matching Procedures: Application to the Admission Post-Baccalaureat Platform

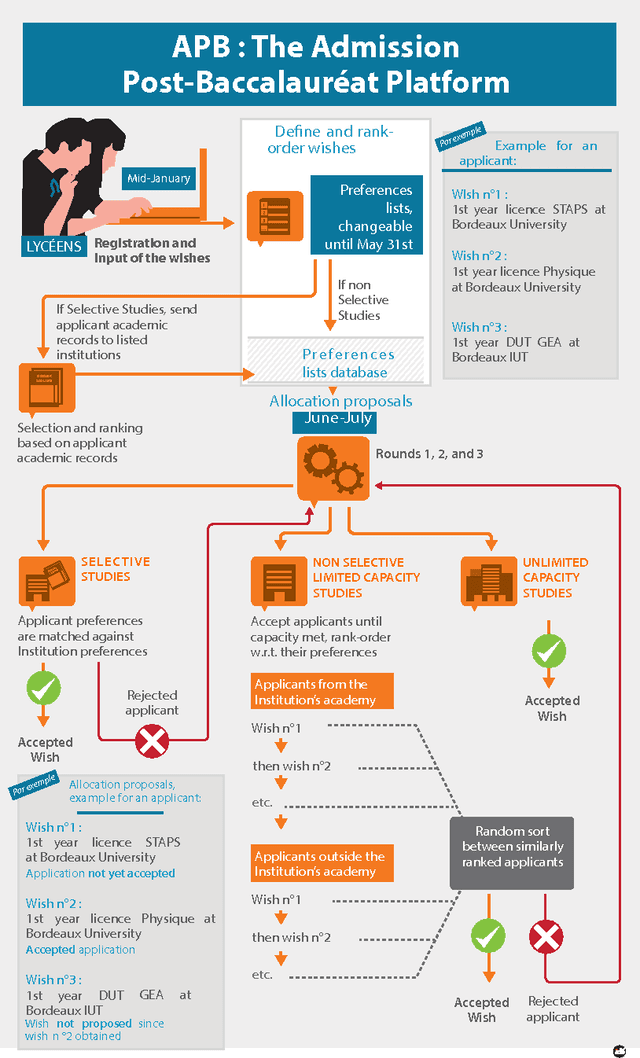
Because preferences naturally arise and play an important role in many real-life decisions, they are at the backbone of various fields. In particular preferences are increasingly used in almost all matching procedures-based applications. In this work we highlight the benefit of using AI insights on preferences in a large scale application, namely the French Admission Post-Baccalaureat Platform (APB). Each year APB allocates hundreds of thousands first year applicants to universities. This is done automatically by matching applicants preferences to university seats. In practice, APB can be unable to distinguish between applicants which leads to the introduction of random selection. This has created frustration in the French public since randomness, even used as a last mean does not fare well with the republican egalitarian principle. In this work, we provide a solution to this problem. We take advantage of recent AI Preferences Theory results to show how to enhance APB in order to improve expressiveness of applicants preferences and reduce their exposure to random decisions.

Abduction and Dialogical Proof in Argumentation and Logic Programming

We develop a model of abduction in abstract argumentation, where changes to an argumentation framework act as hypotheses to explain the support of an observation. We present dialogical proof theories for the main decision problems (i.e., finding hypothe- ses that explain skeptical/credulous support) and we show that our model can be instantiated on the basis of abductive logic programs.

A Principled Analysis of Merging Operations in Possibilistic Logic

Possibilistic logic offers a qualitative framework for representing pieces of information associated with levels of uncertainty of priority. The fusion of multiple sources information is discussed in this setting. Different classes of merging operators are considered including conjunctive, disjunctive, reinforcement, adaptive and averaging operators. Then we propose to analyse these classes in terms of postulates. This is done by first extending the postulate for merging classical bases to the case where priorites are avaialbe.

Graphical readings of possibilistic logic bases

Possibility theory offers either a qualitive, or a numerical framework for representing uncertainty, in terms of dual measures of possibility and necessity. This leads to the existence of two kinds of possibilistic causal graphs where the conditioning is either based on the minimum, or the product operator. Benferhat et al. (1999) have investigated the connections between min-based graphs and possibilistic logic bases (made of classical formulas weighted in terms of certainty). This paper deals with a more difficult issue : the product-based graphical representations of possibilistic bases, which provides an easy structural reading of possibilistic bases. Moreover, this paper also provides another reading of possibilistic bases in terms of comparative preferences of the form "in the context p, q is preferred to not q". This enables us to explicit preferences underlying a set of goals with different levels of priority.

Bipolar Possibilistic Representations

Recently, it has been emphasized that the possibility theory framework allows us to distinguish between i) what is possible because it is not ruled out by the available knowledge, and ii) what is possible for sure. This distinction may be useful when representing knowledge, for modelling values which are not impossible because they are consistent with the available knowledge on the one hand, and values guaranteed to be possible because reported from observations on the other hand. It is also of interest when expressing preferences, to point out values which are positively desired among those which are not rejected. This distinction can be encoded by two types of constraints expressed in terms of necessity measures and in terms of guaranteed possibility functions, which induce a pair of possibility distributions at the semantic level. A consistency condition should ensure that what is claimed to be guaranteed as possible is indeed not impossible. The present paper investigates the representation of this bipolar view, including the case when it is stated by means of conditional measures, or by means of comparative context-dependent constraints. The interest of this bipolar framework, which has been recently stressed for expressing preferences, is also pointed out in the representation of diagnostic knowledge.