Dov Gabbay
Value-based Practical Reasoning: Modal Logic + Argumentation
Apr 11, 2022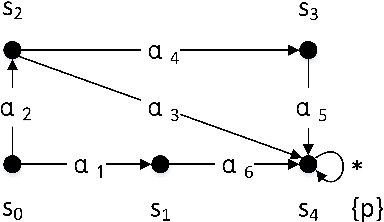
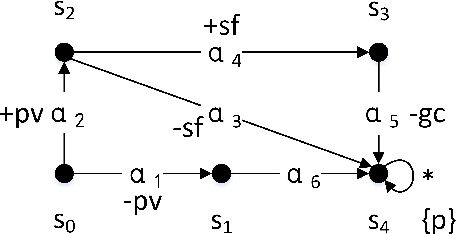
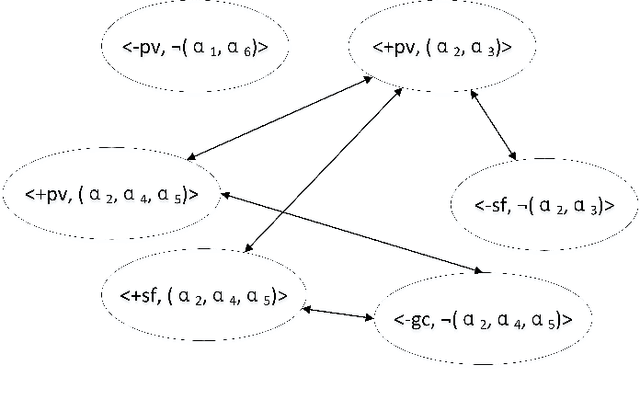
Abstract:Autonomous agents are supposed to be able to finish tasks or achieve goals that are assigned by their users through performing a sequence of actions. Since there might exist multiple plans that an agent can follow and each plan might promote or demote different values along each action, the agent should be able to resolve the conflicts between them and evaluate which plan he should follow. In this paper, we develop a logic-based framework that combines modal logic and argumentation for value-based practical reasoning with plans. Modal logic is used as a technique to represent and verify whether a plan with its local properties of value promotion or demotion can be followed to achieve an agent's goal. We then propose an argumentation-based approach that allows an agent to reason about his plans in the form of supporting or objecting to a plan using the verification results.
BTPK-based learning: An Interpretable Method for Named Entity Recognition
Jan 24, 2022Abstract:Named entity recognition (NER) is an essential task in natural language processing, but the internal mechanism of most NER models is a black box for users. In some high-stake decision-making areas, improving the interpretability of an NER method is crucial but challenging. In this paper, based on the existing Deterministic Talmudic Public announcement logic (TPK) model, we propose a novel binary tree model (called BTPK) and apply it to two widely used Bi-RNNs to obtain BTPK-based interpretable ones. Then, we design a counterfactual verification module to verify the BTPK-based learning method. Experimental results on three public datasets show that the BTPK-based learning outperform two classical Bi-RNNs with self-attention, especially on small, simple data and relatively large, complex data. Moreover, the counterfactual verification demonstrates that the explanations provided by the BTPK-based learning method are reasonable and accurate in NER tasks. Besides, the logical reasoning based on BTPK shows how Bi-RNNs handle NER tasks, with different distance of public announcements on long and complex sequences.
Abduction and Dialogical Proof in Argumentation and Logic Programming
Jul 15, 2014
Abstract:We develop a model of abduction in abstract argumentation, where changes to an argumentation framework act as hypotheses to explain the support of an observation. We present dialogical proof theories for the main decision problems (i.e., finding hypothe- ses that explain skeptical/credulous support) and we show that our model can be instantiated on the basis of abductive logic programs.
Interpolable Formulas in Equilibrium Logic and Answer Set Programming
Jan 16, 2014Abstract:Interpolation is an important property of classical and many non-classical logics that has been shown to have interesting applications in computer science and AI. Here we study the Interpolation Property for the the non-monotonic system of equilibrium logic, establishing weaker or stronger forms of interpolation depending on the precise interpretation of the inference relation. These results also yield a form of interpolation for ground logic programs under the answer sets semantics. For disjunctive logic programs we also study the property of uniform interpolation that is closely related to the concept of variable forgetting. The first-order version of equilibrium logic has analogous Interpolation properties whenever the collection of equilibrium models is (first-order) definable. Since this is the case for so-called safe programs and theories, it applies to the usual situations that arise in practical answer set programming.
Embedding and Automating Conditional Logics in Classical Higher-Order Logic
Aug 17, 2011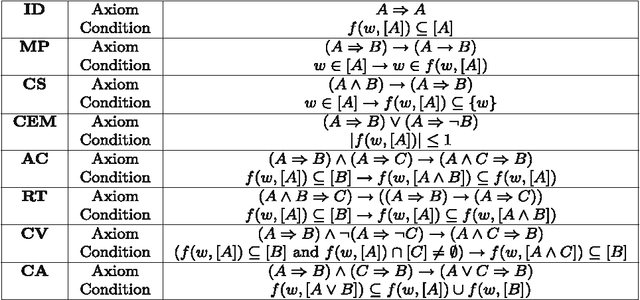
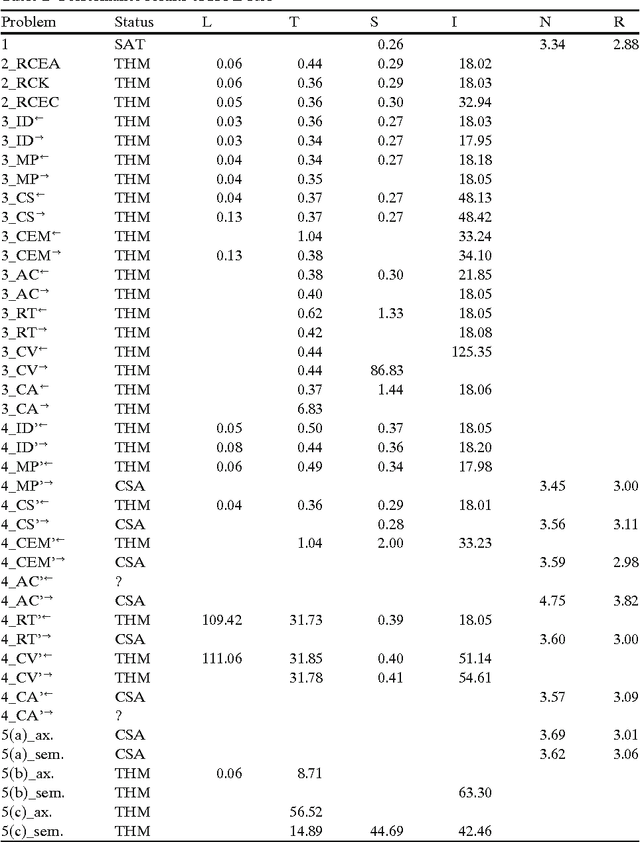
Abstract:A sound and complete embedding of conditional logics into classical higher-order logic is presented. This embedding enables the application of off-the-shelf higher-order automated theorem provers and model finders for reasoning within and about conditional logics.
Interpolation in Equilibrium Logic and Answer Set Programming: the Propositional Case
Dec 17, 2010Abstract:Interpolation is an important property of classical and many non classical logics that has been shown to have interesting applications in computer science and AI. Here we study the Interpolation Property for the propositional version of the non-monotonic system of equilibrium logic, establishing weaker or stronger forms of interpolation depending on the precise interpretation of the inference relation. These results also yield a form of interpolation for ground logic programs under the answer sets semantics. For disjunctive logic programs we also study the property of uniform interpolation that is closely related to the concept of variable forgetting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge