Lectures on Jacques Herbrand as a Logician

We give some lectures on the work on formal logic of Jacques Herbrand, and sketch his life and his influence on automated theorem proving. The intended audience ranges from students interested in logic over historians to logicians. Besides the well-known correction of Herbrand's False Lemma by Goedel and Dreben, we also present the hardly known unpublished correction of Heijenoort and its consequences on Herbrand's Modus Ponens Elimination. Besides Herbrand's Fundamental Theorem and its relation to the Loewenheim-Skolem-Theorem, we carefully investigate Herbrand's notion of intuitionism in connection with his notion of falsehood in an infinite domain. We sketch Herbrand's two proofs of the consistency of arithmetic and his notion of a recursive function, and last but not least, present the correct original text of his unification algorithm with a new translation.

FMLtoHOL (version 1.0): Automating First-order Modal Logics with LEO-II and Friends

A converter from first-order modal logics to classical higher- order logic is presented. This tool enables the application of off-the-shelf higher-order theorem provers and model finders for reasoning within first- order modal logics. The tool supports logics K, K4, D, D4, T, S4, and S5 with respect to constant, varying and cumulative domain semantics.

Quantified Conditional Logics are Fragments of HOL

A semantic embedding of (constant domain) quantified conditional logic in classical higher-order logic is presented.

Embedding and Automating Conditional Logics in Classical Higher-Order Logic

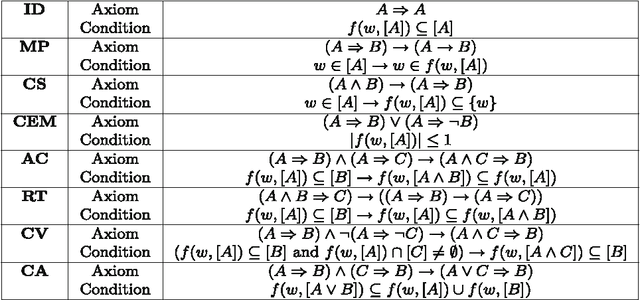
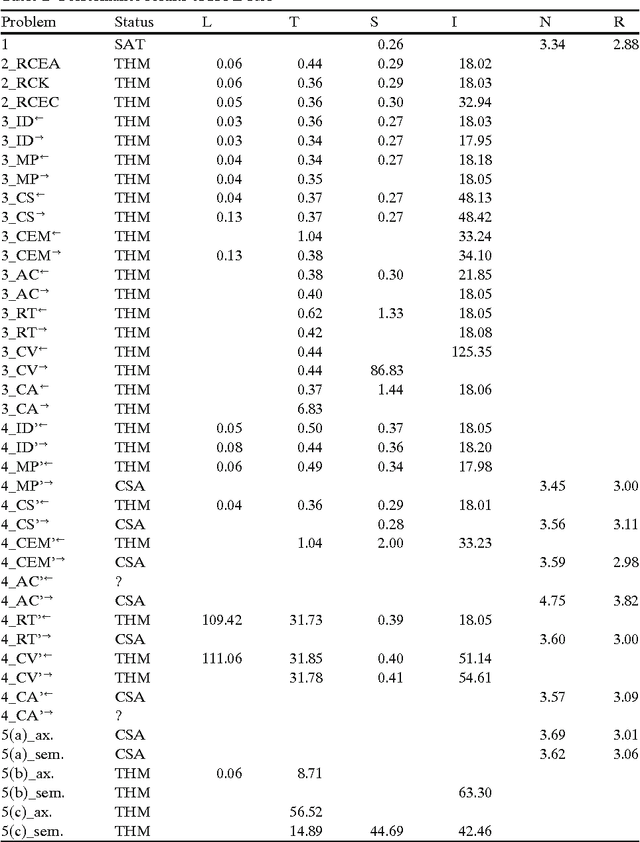
A sound and complete embedding of conditional logics into classical higher-order logic is presented. This embedding enables the application of off-the-shelf higher-order automated theorem provers and model finders for reasoning within and about conditional logics.

Simple Type Theory as Framework for Combining Logics

Simple type theory is suited as framework for combining classical and non-classical logics. This claim is based on the observation that various prominent logics, including (quantified) multimodal logics and intuitionistic logics, can be elegantly embedded in simple type theory. Furthermore, simple type theory is sufficiently expressive to model combinations of embedded logics and it has a well understood semantics. Off-the-shelf reasoning systems for simple type theory exist that can be uniformly employed for reasoning within and about combinations of logics.

Automating Quantified Multimodal Logics in Simple Type Theory -- A Case Study

In a case study we investigate whether off the shelf higher-order theorem provers and model generators can be employed to automate reasoning in and about quantified multimodal logics. In our experiments we exploit the new TPTP infrastructure for classical higher-order logic.

Granularity-Adaptive Proof Presentation

When mathematicians present proofs they usually adapt their explanations to their didactic goals and to the (assumed) knowledge of their addressees. Modern automated theorem provers, in contrast, present proofs usually at a fixed level of detail (also called granularity). Often these presentations are neither intended nor suitable for human use. A challenge therefore is to develop user- and goal-adaptive proof presentation techniques that obey common mathematical practice. We present a flexible and adaptive approach to proof presentation that exploits machine learning techniques to extract a model of the specific granularity of proof examples and employs this model for the automated generation of further proofs at an adapted level of granularity.

Quantified Multimodal Logics in Simple Type Theory

We present a straightforward embedding of quantified multimodal logic in simple type theory and prove its soundness and completeness. Modal operators are replaced by quantification over a type of possible worlds. We present simple experiments, using existing higher-order theorem provers, to demonstrate that the embedding allows automated proofs of statements in these logics, as well as meta properties of them.

Automating Access Control Logics in Simple Type Theory with LEO-II

Garg and Abadi recently proved that prominent access control logics can be translated in a sound and complete way into modal logic S4. We have previously outlined how normal multimodal logics, including monomodal logics K and S4, can be embedded in simple type theory (which is also known as higher-order logic) and we have demonstrated that the higher-order theorem prover LEO-II can automate reasoning in and about them. In this paper we combine these results and describe a sound and complete embedding of different access control logics in simple type theory. Employing this framework we show that the off the shelf theorem prover LEO-II can be applied to automate reasoning in prominent access control logics.

Cut-Simulation and Impredicativity

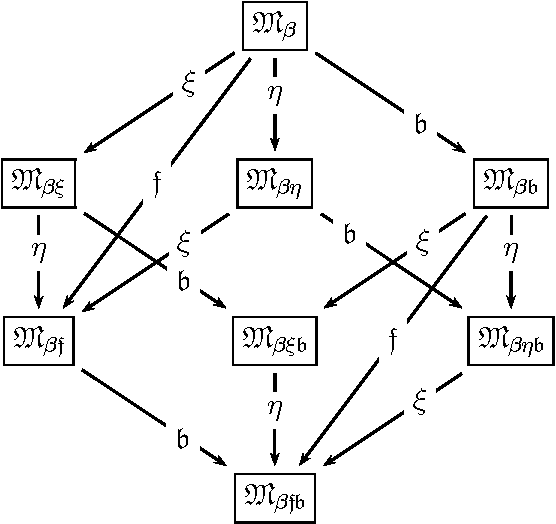
We investigate cut-elimination and cut-simulation in impredicative (higher-order) logics. We illustrate that adding simple axioms such as Leibniz equations to a calculus for an impredicative logic -- in our case a sequent calculus for classical type theory -- is like adding cut. The phenomenon equally applies to prominent axioms like Boolean- and functional extensionality, induction, choice, and description. This calls for the development of calculi where these principles are built-in instead of being treated axiomatically.