Michael Kohlhase
Computer Science, FAU Erlangen-Nürnberg
GF + MMT = GLF -- From Language to Semantics through LF
Oct 24, 2019
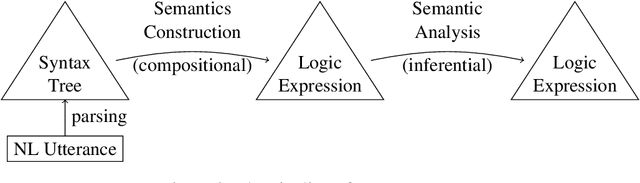


Abstract:These days, vast amounts of knowledge are available online, most of it in written form. Search engines help us access this knowledge, but aggregating, relating and reasoning with it is still a predominantly human effort. One of the key challenges for automated reasoning based on natural-language texts is the need to extract meaning (semantics) from texts. Natural language understanding (NLU) systems describe the conversion from a set of natural language utterances to terms in a particular logic. Tools for the co-development of grammar and target logic are currently largely missing. We will describe the Grammatical Logical Framework (GLF), a combination of two existing frameworks, in which large parts of a symbolic, rule-based NLU system can be developed and implemented: the Grammatical Framework (GF) and MMT. GF is a tool for syntactic analysis, generation, and translation with complex natural language grammars and MMT can be used to specify logical systems and to represent knowledge in them. Combining these tools is possible, because they are based on compatible logical frameworks: Martin-L\"of type theory and LF. The flexibility of logical frameworks is needed, as NLU research has not settled on a particular target logic for meaning representation. Instead, new logics are developed all the time to handle various language phenomena. GLF allows users to develop the logic and the language parsing components in parallel, and to connect them for experimentation with the entire pipeline.
* In Proceedings LFMTP 2019, arXiv:1910.08712
Big Math and the One-Brain Barrier A Position Paper and Architecture Proposal
Apr 23, 2019

Abstract:Over the last decades, a class of important mathematical results have required an ever increasing amount of human effort to carry out. For some, the help of computers is now indispensable. We analyze the implications of this trend towards "big mathematics", its relation to human cognition, and how machine support for big math can be organized. The central contribution of this position paper is an information model for "doing mathematics", which posits that humans very efficiently integrate four aspects: inference, computation, tabulation, and narration around a well-organized core of mathematical knowledge. The challenge for mathematical software systems is that these four aspects need to be integrated as well. We briefly survey the state of the art.
sTeX+ - a System for Flexible Formalization of Linked Data
Jun 23, 2010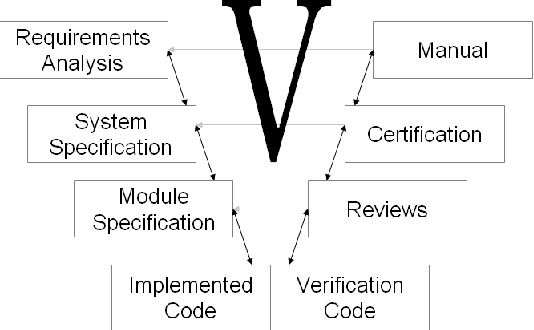



Abstract:We present the sTeX+ system, a user-driven advancement of sTeX - a semantic extension of LaTeX that allows for producing high-quality PDF documents for (proof)reading and printing, as well as semantic XML/OMDoc documents for the Web or further processing. Originally sTeX had been created as an invasive, semantic frontend for authoring XML documents. Here, we used sTeX in a Software Engineering case study as a formalization tool. In order to deal with modular pre-semantic vocabularies and relations, we upgraded it to sTeX+ in a participatory design process. We present a tool chain that starts with an sTeX+ editor and ultimately serves the generated documents as XHTML+RDFa Linked Data via an OMDoc-enabled, versioned XML database. In the final output, all structural annotations are preserved in order to enable semantic information retrieval services.
Dimensions of Formality: A Case Study for MKM in Software Engineering
Apr 28, 2010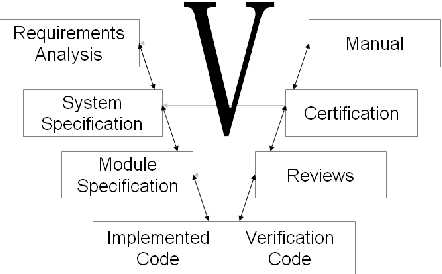

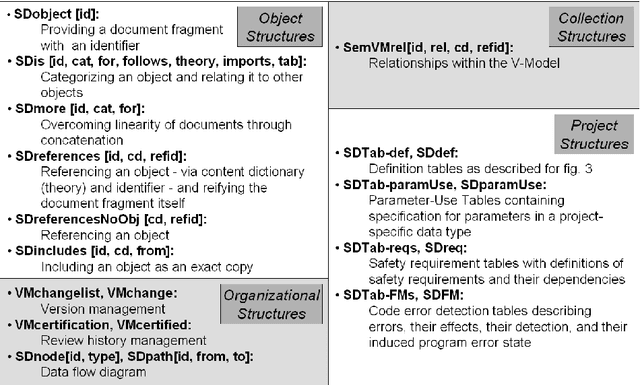

Abstract:We study the formalization of a collection of documents created for a Software Engineering project from an MKM perspective. We analyze how document and collection markup formats can cope with an open-ended, multi-dimensional space of primary and secondary classifications and relationships. We show that RDFa-based extensions of MKM formats, employing flexible "metadata" relationships referencing specific vocabularies for distinct dimensions, are well-suited to encode this and to put it into service. This formalized knowledge can be used for enriching interactive document browsing, for enabling multi-dimensional metadata queries over documents and collections, and for exporting Linked Data to the Semantic Web and thus enabling further reuse.
Publishing Math Lecture Notes as Linked Data
Apr 20, 2010Abstract:We mark up a corpus of LaTeX lecture notes semantically and expose them as Linked Data in XHTML+MathML+RDFa. Our application makes the resulting documents interactively browsable for students. Our ontology helps to answer queries from students and lecturers, and paves the path towards an integration of our corpus with external sites.
Cut-Simulation and Impredicativity
Mar 02, 2009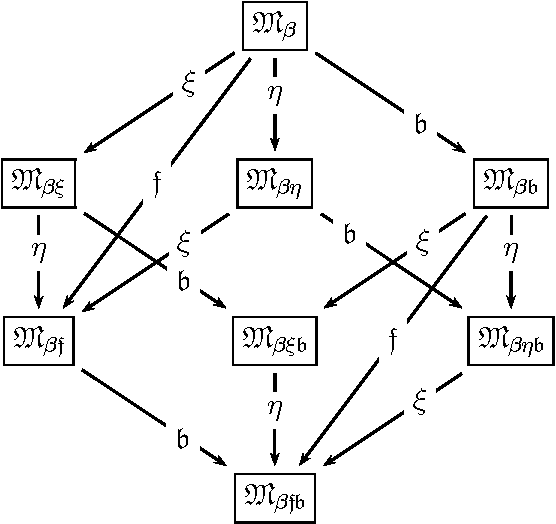

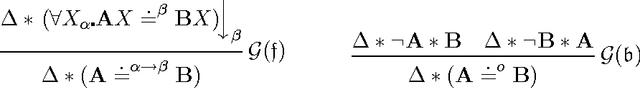
Abstract:We investigate cut-elimination and cut-simulation in impredicative (higher-order) logics. We illustrate that adding simple axioms such as Leibniz equations to a calculus for an impredicative logic -- in our case a sequent calculus for classical type theory -- is like adding cut. The phenomenon equally applies to prominent axioms like Boolean- and functional extensionality, induction, choice, and description. This calls for the development of calculi where these principles are built-in instead of being treated axiomatically.
* 21 pages
Computing Parallelism in Discourse
May 01, 1997
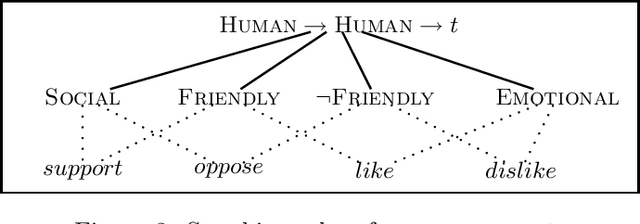


Abstract:Although much has been said about parallelism in discourse, a formal, computational theory of parallelism structure is still outstanding. In this paper, we present a theory which given two parallel utterances predicts which are the parallel elements. The theory consists of a sorted, higher-order abductive calculus and we show that it reconciles the insights of discourse theories of parallelism with those of Higher-Order Unification approaches to discourse semantics, thereby providing a natural framework in which to capture the effect of parallelism on discourse semantics.
* 6 pages
Corrections and Higher-Order Unification
Sep 02, 1996Abstract:We propose an analysis of corrections which models some of the requirements corrections place on context. We then show that this analysis naturally extends to the interaction of corrections with pronominal anaphora on the one hand, and (in)definiteness on the other. The analysis builds on previous unification--based approaches to NL semantics and relies on Higher--Order Unification with Equivalences, a form of unification which takes into account not only syntactic beta-eta-identity but also denotational equivalence.
Focus and Higher-Order Unification
May 02, 1996Abstract:Pulman has shown that Higher--Order Unification (HOU) can be used to model the interpretation of focus. In this paper, we extend the unification--based approach to cases which are often seen as a test--bed for focus theory: utterances with multiple focus operators and second occurrence expressions. We then show that the resulting analysis favourably compares with two prominent theories of focus (namely, Rooth's Alternative Semantics and Krifka's Structured Meanings theory) in that it correctly generates interpretations which these alternative theories cannot yield. Finally, we discuss the formal properties of the approach and argue that even though HOU need not terminate, for the class of unification--problems dealt with in this paper, HOU avoids this shortcoming and is in fact computationally tractable.
Higher-Order Coloured Unification and Natural Language Semantics
May 02, 1996Abstract:In this paper, we show that Higher-Order Coloured Unification - a form of unification developed for automated theorem proving - provides a general theory for modeling the interface between the interpretation process and other sources of linguistic, non semantic information. In particular, it provides the general theory for the Primary Occurrence Restriction which (Dalrymple, Shieber and Pereira, 1991)'s analysis called for.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge