Experiments with Choice in Dependently-Typed Higher-Order Logic

Recently an extension to higher-order logic -- called DHOL -- was introduced, enriching the language with dependent types, and creating a powerful extensional type theory. In this paper we propose two ways how choice can be added to DHOL. We extend the DHOL term structure by Hilbert's indefinite choice operator $\epsilon$, define a translation of the choice terms to HOL choice that extends the existing translation from DHOL to HOL and show that the extension of the translation is complete and give an argument for soundness. We finally evaluate the extended translation on a set of dependent HOL problems that require choice.

Prolog Technology Reinforcement Learning Prover

We present a reinforcement learning toolkit for experiments with guiding automated theorem proving in the connection calculus. The core of the toolkit is a compact and easy to extend Prolog-based automated theorem prover called plCoP. plCoP builds on the leanCoP Prolog implementation and adds learning-guided Monte-Carlo Tree Search as done in the rlCoP system. Other components include a Python interface to plCoP and machine learners, and an external proof checker that verifies the validity of plCoP proofs. The toolkit is evaluated on two benchmarks and we demonstrate its extendability by two additions: (1) guidance is extended to reduction steps and (2) the standard leanCoP calculus is extended with rewrite steps and their learned guidance. We argue that the Prolog setting is suitable for combining statistical and symbolic learning methods. The complete toolkit is publicly released.

Self-Learned Formula Synthesis in Set Theory

A reinforcement learning algorithm accomplishes the task of synthesizing a set-theoretical formula that evaluates to given truth values for given assignments.

Can Neural Networks Learn Symbolic Rewriting?

This work investigates if the current neural architectures are adequate for learning symbolic rewriting. Two kinds of data sets are proposed for this research -- one based on automated proofs and the other being a synthetic set of polynomial terms. The experiments with use of the current neural machine translation models are performed and its results are discussed. Ideas for extending this line of research are proposed and its relevance is motivated.

Cut-Simulation and Impredicativity

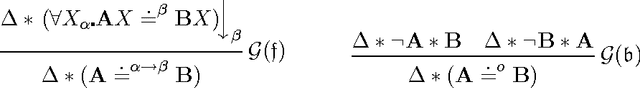
We investigate cut-elimination and cut-simulation in impredicative (higher-order) logics. We illustrate that adding simple axioms such as Leibniz equations to a calculus for an impredicative logic -- in our case a sequent calculus for classical type theory -- is like adding cut. The phenomenon equally applies to prominent axioms like Boolean- and functional extensionality, induction, choice, and description. This calls for the development of calculi where these principles are built-in instead of being treated axiomatically.