Learning Conjecturing from Scratch

We develop a self-learning approach for conjecturing of induction predicates on a dataset of 16197 problems derived from the OEIS. These problems are hard for today's SMT and ATP systems because they require a combination of inductive and arithmetical reasoning. Starting from scratch, our approach consists of a feedback loop that iterates between (i) training a neural translator to learn the correspondence between the problems solved so far and the induction predicates useful for them, (ii) using the trained neural system to generate many new induction predicates for the problems, (iii) fast runs of the z3 prover attempting to prove the problems using the generated predicates, (iv) using heuristics such as predicate size and solution speed on the proved problems to choose the best predicates for the next iteration of training. The algorithm discovers on its own many interesting induction predicates, ultimately solving 5565 problems, compared to 2265 problems solved by CVC5, Vampire or Z3 in 60 seconds.

Machine Learning for Quantifier Selection in cvc5

In this work we considerably improve the state-of-the-art SMT solving on first-order quantified problems by efficient machine learning guidance of quantifier selection. Quantifiers represent a significant challenge for SMT and are technically a source of undecidability. In our approach, we train an efficient machine learning model that informs the solver which quantifiers should be instantiated and which not. Each quantifier may be instantiated multiple times and the set of the active quantifiers changes as the solving progresses. Therefore, we invoke the ML predictor many times, during the whole run of the solver. To make this efficient, we use fast ML models based on gradient boosting decision trees. We integrate our approach into the state-of-the-art cvc5 SMT solver and show a considerable increase of the system's holdout-set performance after training it on a large set of first-order problems collected from the Mizar Mathematical Library.

Solving Hard Mizar Problems with Instantiation and Strategy Invention

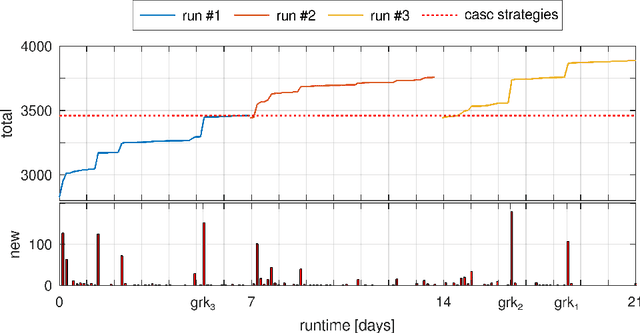
In this work, we prove over 3000 previously ATP-unproved Mizar/MPTP problems by using several ATP and AI methods, raising the number of ATP-solved Mizar problems from 75\% to above 80\%. First, we start to experiment with the cvc5 SMT solver which uses several instantiation-based heuristics that differ from the superposition-based systems, that were previously applied to Mizar,and add many new solutions. Then we use automated strategy invention to develop cvc5 strategies that largely improve cvc5's performance on the hard problems. In particular, the best invented strategy solves over 14\% more problems than the best previously available cvc5 strategy. We also show that different clausification methods have a high impact on such instantiation-based methods, again producing many new solutions. In total, the methods solve 3021 (21.3\%) of the 14163 previously unsolved hard Mizar problems. This is a new milestone over the Mizar large-theory benchmark and a large strengthening of the hammer methods for Mizar.

Learning Guided Automated Reasoning: A Brief Survey

Automated theorem provers and formal proof assistants are general reasoning systems that are in theory capable of proving arbitrarily hard theorems, thus solving arbitrary problems reducible to mathematics and logical reasoning. In practice, such systems however face large combinatorial explosion, and therefore include many heuristics and choice points that considerably influence their performance. This is an opportunity for trained machine learning predictors, which can guide the work of such reasoning systems. Conversely, deductive search supported by the notion of logically valid proof allows one to train machine learning systems on large reasoning corpora. Such bodies of proof are usually correct by construction and when combined with more and more precise trained guidance they can be boostrapped into very large corpora, with increasingly long reasoning chains and possibly novel proof ideas. In this paper we provide an overview of several automated reasoning and theorem proving domains and the learning and AI methods that have been so far developed for them. These include premise selection, proof guidance in several settings, AI systems and feedback loops iterating between reasoning and learning, and symbolic classification problems.

Translating SUMO-K to Higher-Order Set Theory

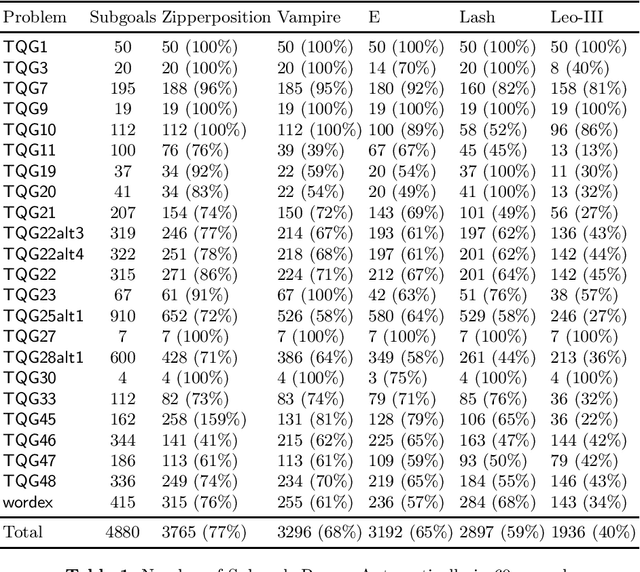
We describe a translation from a fragment of SUMO (SUMO-K) into higher-order set theory. The translation provides a formal semantics for portions of SUMO which are beyond first-order and which have previously only had an informal interpretation. It also for the first time embeds a large common-sense ontology into a very secure interactive theorem proving system. We further extend our previous work in finding contradictions in SUMO from first order constructs to include a portion of SUMO's higher order constructs. Finally, using the translation, we can create problems that can be proven using higher-order interactive and automated theorem provers. This is tested in several systems and can be used to form a corpus of higher-order common-sense reasoning problems.

MizAR 60 for Mizar 50

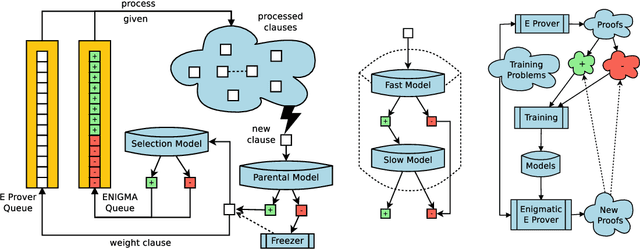
As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

Alien Coding

We introduce a self-learning algorithm for synthesizing programs for OEIS sequences. The algorithm starts from scratch initially generating programs at random. Then it runs many iterations of a self-learning loop that interleaves (i) training neural machine translation to learn the correspondence between sequences and the programs discovered so far, and (ii) proposing many new programs for each OEIS sequence by the trained neural machine translator. The algorithm discovers on its own programs for more than 78000 OEIS sequences, sometimes developing unusual programming methods. We analyze its behavior and the invented programs in several experiments.

Machine Learning Meets The Herbrand Universe

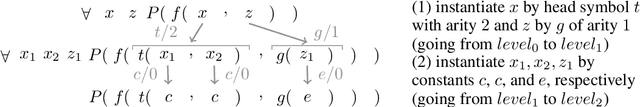
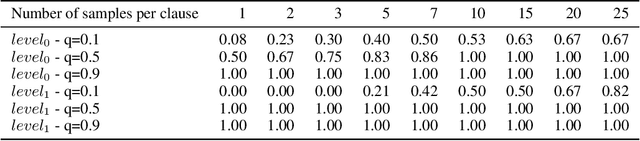
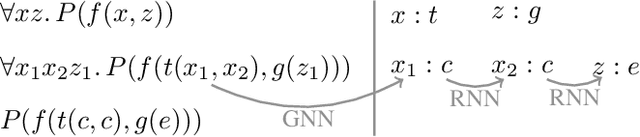
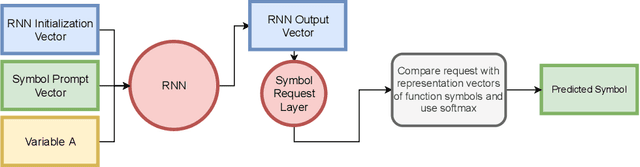
The appearance of strong CDCL-based propositional (SAT) solvers has greatly advanced several areas of automated reasoning (AR). One of the directions in AR is thus to apply SAT solvers to expressive formalisms such as first-order logic, for which large corpora of general mathematical problems exist today. This is possible due to Herbrand's theorem, which allows reduction of first-order problems to propositional problems by instantiation. The core challenge is choosing the right instances from the typically infinite Herbrand universe. In this work, we develop the first machine learning system targeting this task, addressing its combinatorial and invariance properties. In particular, we develop a GNN2RNN architecture based on an invariant graph neural network (GNN) that learns from problems and their solutions independently of symbol names (addressing the abundance of skolems), combined with a recurrent neural network (RNN) that proposes for each clause its instantiations. The architecture is then trained on a corpus of mathematical problems and their instantiation-based proofs, and its performance is evaluated in several ways. We show that the trained system achieves high accuracy in predicting the right instances, and that it is capable of solving many problems by educated guessing when combined with a ground solver. To our knowledge, this is the first convincing use of machine learning in synthesizing relevant elements from arbitrary Herbrand universes.

The Isabelle ENIGMA

We significantly improve the performance of the E automated theorem prover on the Isabelle Sledgehammer problems by combining learning and theorem proving in several ways. In particular, we develop targeted versions of the ENIGMA guidance for the Isabelle problems, targeted versions of neural premise selection, and targeted strategies for E. The methods are trained in several iterations over hundreds of thousands untyped and typed first-order problems extracted from Isabelle. Our final best single-strategy ENIGMA and premise selection system improves the best previous version of E by 25.3% in 15 seconds, outperforming also all other previous ATP and SMT systems.

Learning Theorem Proving Components

Saturation-style automated theorem provers (ATPs) based on the given clause procedure are today the strongest general reasoners for classical first-order logic. The clause selection heuristics in such systems are, however, often evaluating clauses in isolation, ignoring other clauses. This has changed recently by equipping the E/ENIGMA system with a graph neural network (GNN) that chooses the next given clause based on its evaluation in the context of previously selected clauses. In this work, we describe several algorithms and experiments with ENIGMA, advancing the idea of contextual evaluation based on learning important components of the graph of clauses.