Inference in Partially Linear Models under Dependent Data with Deep Neural Networks

I consider inference in a partially linear regression model under stationary $\beta$-mixing data after first stage deep neural network (DNN) estimation. Using the DNN results of Brown (2024), I show that the estimator for the finite dimensional parameter, constructed using DNN-estimated nuisance components, achieves $\sqrt{n}$-consistency and asymptotic normality. By avoiding sample splitting, I address one of the key challenges in applying machine learning techniques to econometric models with dependent data. In a future version of this work, I plan to extend these results to obtain general conditions for semiparametric inference after DNN estimation of nuisance components, which will allow for considerations such as more efficient estimation procedures, and instrumental variable settings.

Statistical Properties of Deep Neural Networks with Dependent Data

This paper establishes statistical properties of deep neural network (DNN) estimators under dependent data. Two general results for nonparametric sieve estimators directly applicable to DNNs estimators are given. The first establishes rates for convergence in probability under nonstationary data. The second provides non-asymptotic probability bounds on $\mathcal{L}^{2}$-errors under stationary $\beta$-mixing data. I apply these results to DNN estimators in both regression and classification contexts imposing only a standard H\"older smoothness assumption. These results are then used to demonstrate how asymptotic inference can be conducted on the finite dimensional parameter of a partially linear regression model after first-stage DNN estimation of infinite dimensional parameters. The DNN architectures considered are common in applications, featuring fully connected feedforward networks with any continuous piecewise linear activation function, unbounded weights, and a width and depth that grows with sample size. The framework provided also offers potential for research into other DNN architectures and time-series applications.

Translating SUMO-K to Higher-Order Set Theory

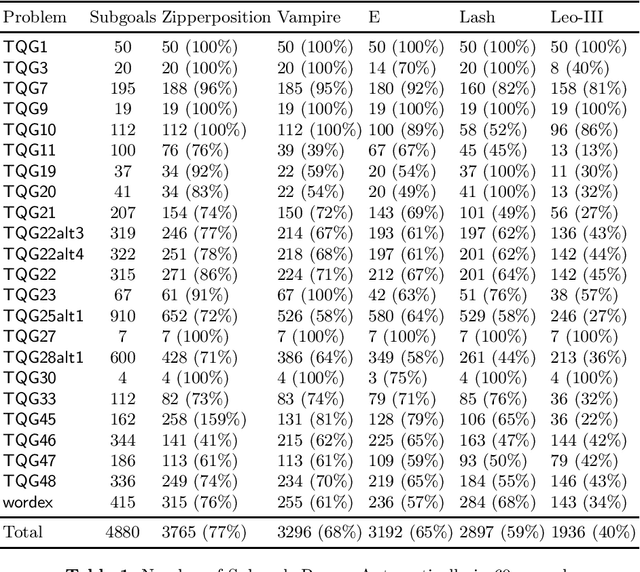
We describe a translation from a fragment of SUMO (SUMO-K) into higher-order set theory. The translation provides a formal semantics for portions of SUMO which are beyond first-order and which have previously only had an informal interpretation. It also for the first time embeds a large common-sense ontology into a very secure interactive theorem proving system. We further extend our previous work in finding contradictions in SUMO from first order constructs to include a portion of SUMO's higher order constructs. Finally, using the translation, we can create problems that can be proven using higher-order interactive and automated theorem provers. This is tested in several systems and can be used to form a corpus of higher-order common-sense reasoning problems.

Exploration of Neural Machine Translation in Autoformalization of Mathematics in Mizar

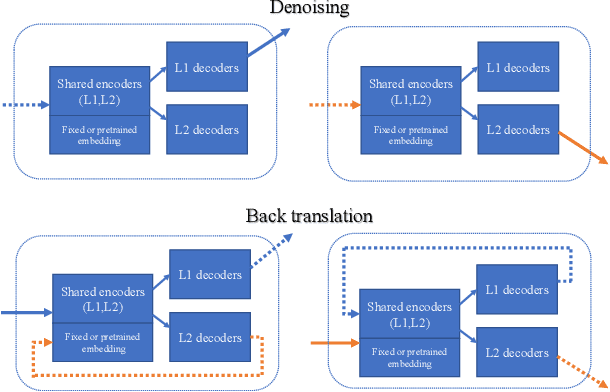
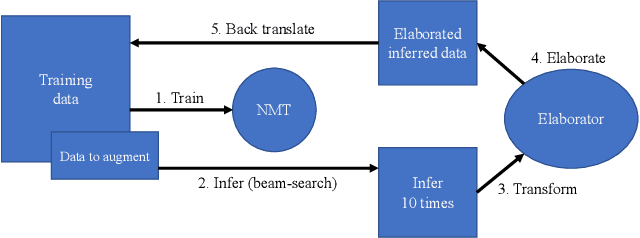
In this paper we share several experiments trying to automatically translate informal mathematics into formal mathematics. In our context informal mathematics refers to human-written mathematical sentences in the LaTeX format; and formal mathematics refers to statements in the Mizar language. We conducted our experiments against three established neural network-based machine translation models that are known to deliver competitive results on translating between natural languages. To train these models we also prepared four informal-to-formal datasets. We compare and analyze our results according to whether the model is supervised or unsupervised. In order to augment the data available for auto-formalization and improve the results, we develop a custom type-elaboration mechanism and integrate it in the supervised translation.

Internal Guidance for Satallax

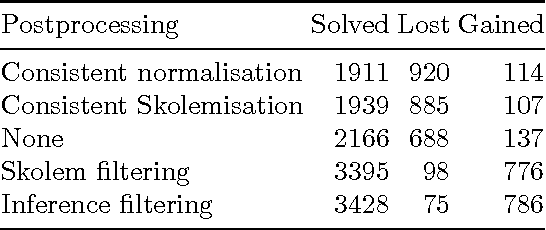
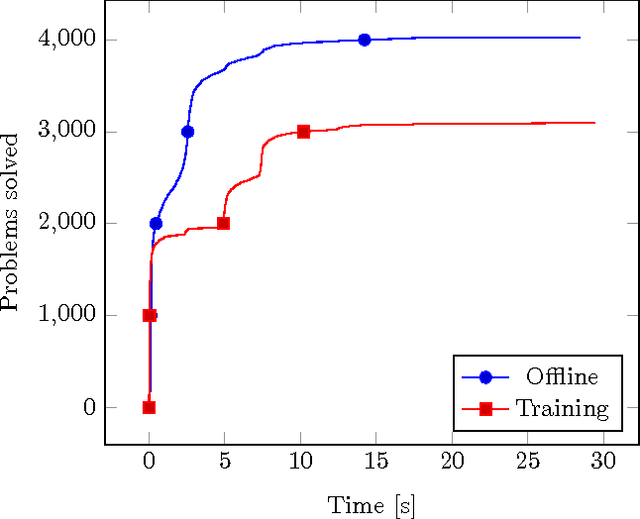
We propose a new internal guidance method for automated theorem provers based on the given-clause algorithm. Our method influences the choice of unprocessed clauses using positive and negative examples from previous proofs. To this end, we present an efficient scheme for Naive Bayesian classification by generalising label occurrences to types with monoid structure. This makes it possible to extend existing fast classifiers, which consider only positive examples, with negative ones. We implement the method in the higher-order logic prover Satallax, where we modify the delay with which propositions are processed. We evaluated our method on a simply-typed higher-order logic version of the Flyspeck project, where it solves 26% more problems than Satallax without internal guidance.

Extracting Higher-Order Goals from the Mizar Mathematical Library

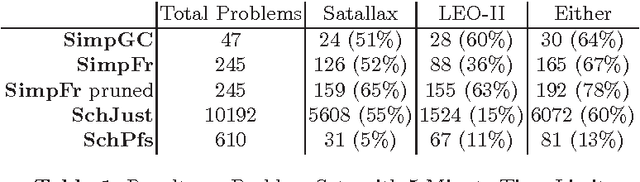
Certain constructs allowed in Mizar articles cannot be represented in first-order logic but can be represented in higher-order logic. We describe a way to obtain higher-order theorem proving problems from Mizar articles that make use of these constructs. In particular, higher-order logic is used to represent schemes, a global choice construct and set level binders. The higher-order automated theorem provers Satallax and LEO-II have been run on collections of these problems and the results are discussed.