Extracting Higher-Order Goals from the Mizar Mathematical Library
Paper and Code
May 23, 2016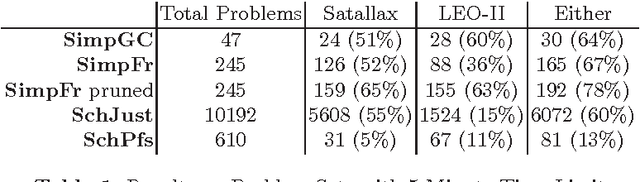
Certain constructs allowed in Mizar articles cannot be represented in first-order logic but can be represented in higher-order logic. We describe a way to obtain higher-order theorem proving problems from Mizar articles that make use of these constructs. In particular, higher-order logic is used to represent schemes, a global choice construct and set level binders. The higher-order automated theorem provers Satallax and LEO-II have been run on collections of these problems and the results are discussed.
* Accepted to CICM 2016. The final publication will be available at
Springer
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge