Geometric Reasoning in the Embedding Space

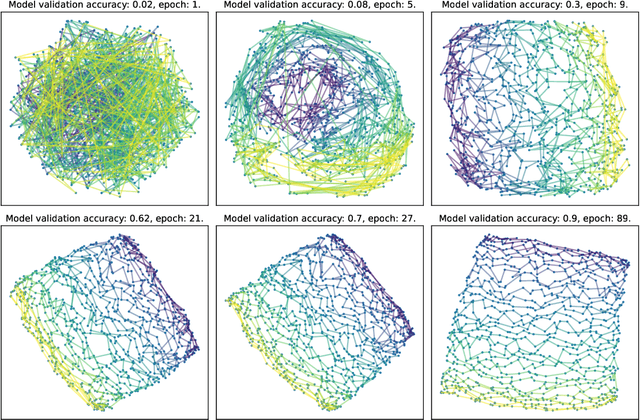
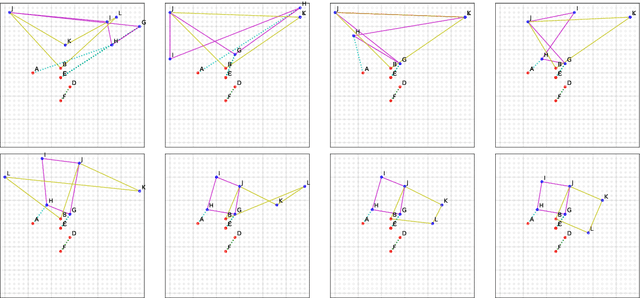
In this contribution, we demonstrate that Graph Neural Networks and Transformers can learn to reason about geometric constraints. We train them to predict spatial position of points in a discrete 2D grid from a set of constraints that uniquely describe hidden figures containing these points. Both models are able to predict the position of points and interestingly, they form the hidden figures described by the input constraints in the embedding space during the reasoning process. Our analysis shows that both models recover the grid structure during training so that the embeddings corresponding to the points within the grid organize themselves in a 2D subspace and reflect the neighborhood structure of the grid. We also show that the Graph Neural Network we design for the task performs significantly better than the Transformer and is also easier to scale.

Neural Approaches to SAT Solving: Design Choices and Interpretability

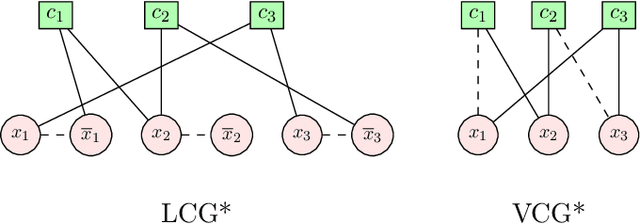
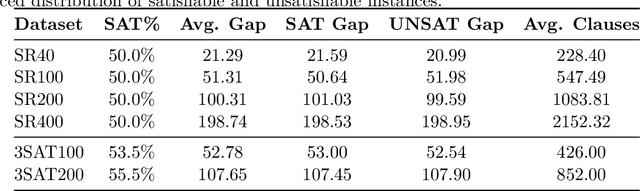
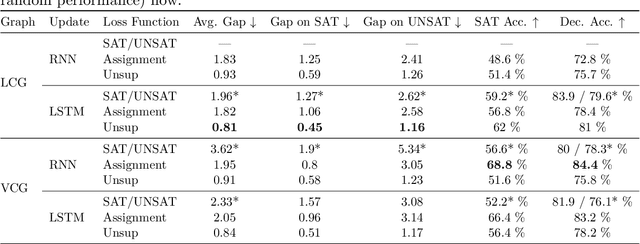
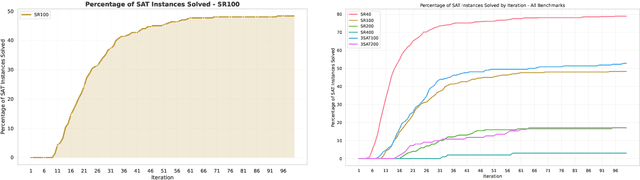
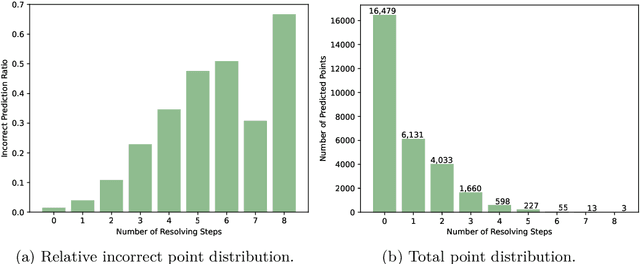
In this contribution, we provide a comprehensive evaluation of graph neural networks applied to Boolean satisfiability problems, accompanied by an intuitive explanation of the mechanisms enabling the model to generalize to different instances. We introduce several training improvements, particularly a novel closest assignment supervision method that dynamically adapts to the model's current state, significantly enhancing performance on problems with larger solution spaces. Our experiments demonstrate the suitability of variable-clause graph representations with recurrent neural network updates, which achieve good accuracy on SAT assignment prediction while reducing computational demands. We extend the base graph neural network into a diffusion model that facilitates incremental sampling and can be effectively combined with classical techniques like unit propagation. Through analysis of embedding space patterns and optimization trajectories, we show how these networks implicitly perform a process very similar to continuous relaxations of MaxSAT, offering an interpretable view of their reasoning process. This understanding guides our design choices and explains the ability of recurrent architectures to scale effectively at inference time beyond their training distribution, which we demonstrate with test-time scaling experiments.

Understanding GNNs for Boolean Satisfiability through Approximation Algorithms

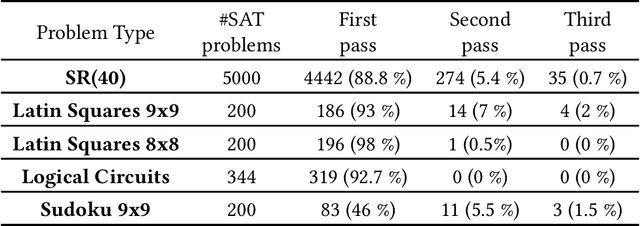
The paper deals with the interpretability of Graph Neural Networks in the context of Boolean Satisfiability. The goal is to demystify the internal workings of these models and provide insightful perspectives into their decision-making processes. This is done by uncovering connections to two approximation algorithms studied in the domain of Boolean Satisfiability: Belief Propagation and Semidefinite Programming Relaxations. Revealing these connections has empowered us to introduce a suite of impactful enhancements. The first significant enhancement is a curriculum training procedure, which incrementally increases the problem complexity in the training set, together with increasing the number of message passing iterations of the Graph Neural Network. We show that the curriculum, together with several other optimizations, reduces the training time by more than an order of magnitude compared to the baseline without the curriculum. Furthermore, we apply decimation and sampling of initial embeddings, which significantly increase the percentage of solved problems.

Machine Learning for Quantifier Selection in cvc5

In this work we considerably improve the state-of-the-art SMT solving on first-order quantified problems by efficient machine learning guidance of quantifier selection. Quantifiers represent a significant challenge for SMT and are technically a source of undecidability. In our approach, we train an efficient machine learning model that informs the solver which quantifiers should be instantiated and which not. Each quantifier may be instantiated multiple times and the set of the active quantifiers changes as the solving progresses. Therefore, we invoke the ML predictor many times, during the whole run of the solver. To make this efficient, we use fast ML models based on gradient boosting decision trees. We integrate our approach into the state-of-the-art cvc5 SMT solver and show a considerable increase of the system's holdout-set performance after training it on a large set of first-order problems collected from the Mizar Mathematical Library.

CFaults: Model-Based Diagnosis for Fault Localization in C Programs with Multiple Test Cases

Debugging is one of the most time-consuming and expensive tasks in software development. Several formula-based fault localization (FBFL) methods have been proposed, but they fail to guarantee a set of diagnoses across all failing tests or may produce redundant diagnoses that are not subset-minimal, particularly for programs with multiple faults. This paper introduces a novel fault localization approach for C programs with multiple faults. CFaults leverages Model-Based Diagnosis (MBD) with multiple observations and aggregates all failing test cases into a unified MaxSAT formula. Consequently, our method guarantees consistency across observations and simplifies the fault localization procedure. Experimental results on two benchmark sets of C programs, TCAS and C-Pack-IPAs, show that CFaults is faster than other FBFL approaches like BugAssist and SNIPER. Moreover, CFaults only generates subset-minimal diagnoses of faulty statements, whereas the other approaches tend to enumerate redundant diagnoses.

Solving Hard Mizar Problems with Instantiation and Strategy Invention

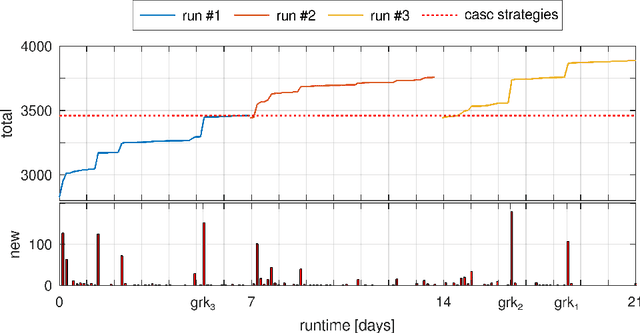
In this work, we prove over 3000 previously ATP-unproved Mizar/MPTP problems by using several ATP and AI methods, raising the number of ATP-solved Mizar problems from 75\% to above 80\%. First, we start to experiment with the cvc5 SMT solver which uses several instantiation-based heuristics that differ from the superposition-based systems, that were previously applied to Mizar,and add many new solutions. Then we use automated strategy invention to develop cvc5 strategies that largely improve cvc5's performance on the hard problems. In particular, the best invented strategy solves over 14\% more problems than the best previously available cvc5 strategy. We also show that different clausification methods have a high impact on such instantiation-based methods, again producing many new solutions. In total, the methods solve 3021 (21.3\%) of the 14163 previously unsolved hard Mizar problems. This is a new milestone over the Mizar large-theory benchmark and a large strengthening of the hammer methods for Mizar.

Graph Neural Networks For Mapping Variables Between Programs -- Extended Version

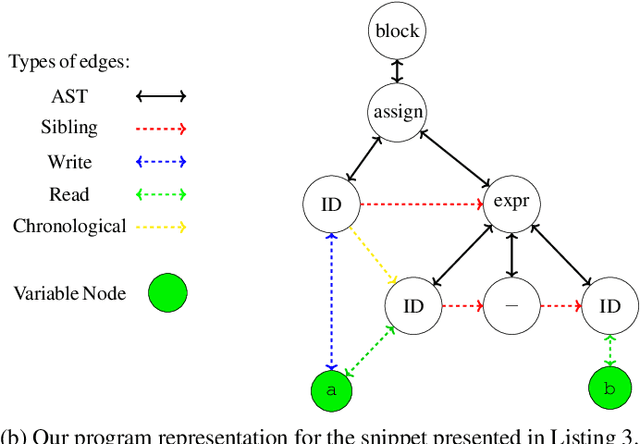
Automated program analysis is a pivotal research domain in many areas of Computer Science -- Formal Methods and Artificial Intelligence, in particular. Due to the undecidability of the problem of program equivalence, comparing two programs is highly challenging. Typically, in order to compare two programs, a relation between both programs' sets of variables is required. Thus, mapping variables between two programs is useful for a panoply of tasks such as program equivalence, program analysis, program repair, and clone detection. In this work, we propose using graph neural networks (GNNs) to map the set of variables between two programs based on both programs' abstract syntax trees (ASTs). To demonstrate the strength of variable mappings, we present three use-cases of these mappings on the task of program repair to fix well-studied and recurrent bugs among novice programmers in introductory programming assignments (IPAs). Experimental results on a dataset of 4166 pairs of incorrect/correct programs show that our approach correctly maps 83% of the evaluation dataset. Moreover, our experiments show that the current state-of-the-art on program repair, greatly dependent on the programs' structure, can only repair about 72% of the incorrect programs. In contrast, our approach, which is solely based on variable mappings, can repair around 88.5%.

InvAASTCluster: On Applying Invariant-Based Program Clustering to Introductory Programming Assignments

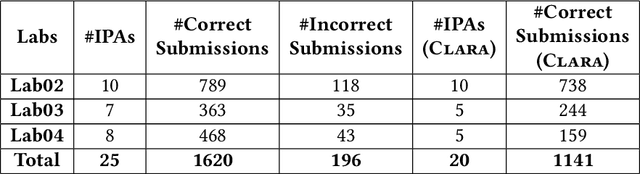
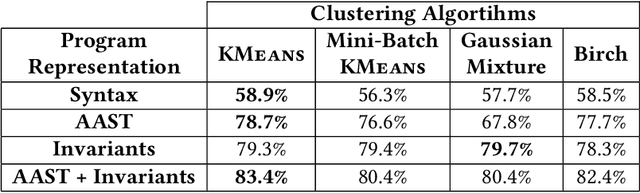
Due to the vast number of students enrolled in Massive Open Online Courses (MOOCs), there has been an increasing number of automated program repair techniques focused on introductory programming assignments (IPAs). Such state-of-the-art techniques use program clustering to take advantage of previous correct student implementations to repair a given new incorrect submission. Usually, these repair techniques use clustering methods since analyzing all available correct student submissions to repair a program is not feasible. The clustering methods use program representations based on several features such as abstract syntax tree (AST), syntax, control flow, and data flow. However, these features are sometimes brittle when representing semantically similar programs. This paper proposes InvAASTCluster, a novel approach for program clustering that takes advantage of dynamically generated program invariants observed over several program executions to cluster semantically equivalent IPAs. Our main objective is to find a more suitable representation of programs using a combination of the program's semantics, through its invariants, and its structure, through its anonymized abstract syntax tree. The evaluation of InvAASTCluster shows that the proposed program representation outperforms syntax-based representations when clustering a set of different correct IPAs. Furthermore, we integrate InvAASTCluster into a state-of-the-art clustering-based program repair tool and evaluate it on a set of IPAs. Our results show that InvAASTCluster advances the current state-of-the-art when used by clustering-based program repair tools by repairing a larger number of students' programs in a shorter amount of time.

C-Pack of IPAs: A C90 Program Benchmark of Introductory Programming Assignments

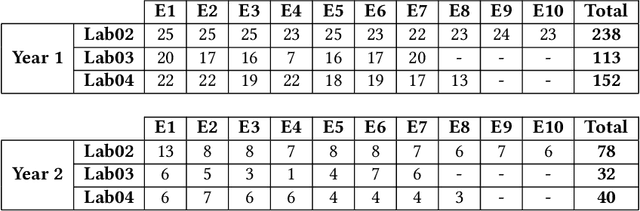
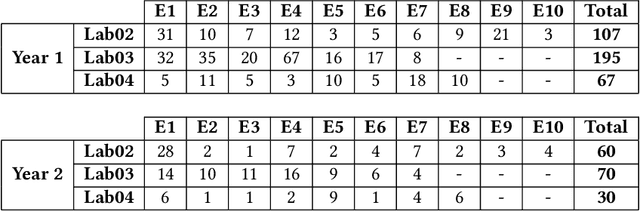
Due to the vast number of students enrolled in Massive Open Online Courses (MOOCs), there has been an increasing number of automated program repair techniques focused on introductory programming assignments (IPAs). Such techniques take advantage of previous correct student implementations in order to provide automated, comprehensive, and personalized feedback to students. This paper presents C-Pack-IPAs, a publicly available benchmark of students' programs submitted for 25 different IPAs. C-Pack-IPAs contains semantically correct, semantically incorrect, and syntactically incorrect programs plus a test suite for each IPA. Hence, C-Pack-IPAs can be used to help evaluate the development of novel semantic, as well as syntactic, automated program repair frameworks, focused on providing feedback to novice programmers.

Fair and Adventurous Enumeration of Quantifier Instantiations

SMT solvers generally tackle quantifiers by instantiating their variables with tuples of terms from the ground part of the formula. Recent enumerative approaches for quantifier instantiation consider tuples of terms in some heuristic order. This paper studies different strategies to order such tuples and their impact on performance. We decouple the ordering problem into two parts. First is the order of the sequence of terms to consider for each quantified variable, and second is the order of the instantiation tuples themselves. While the most and least preferred tuples, i.e. those with all variables assigned to the most or least preferred terms, are clear, the combinations in between allow flexibility in an implementation. We look at principled strategies of complete enumeration, where some strategies are more fair, meaning they treat all the variables the same but some strategies may be more adventurous, meaning that they may venture further down the preference list. We further describe new techniques for discarding irrelevant instantiations which are crucial for the performance of these strategies in practice. These strategies are implemented in the SMT solver cvc5, where they contribute to the diversification of the solver's configuration space, as shown by our experimental results.