Geometric Reasoning in the Embedding Space

In this contribution, we demonstrate that Graph Neural Networks and Transformers can learn to reason about geometric constraints. We train them to predict spatial position of points in a discrete 2D grid from a set of constraints that uniquely describe hidden figures containing these points. Both models are able to predict the position of points and interestingly, they form the hidden figures described by the input constraints in the embedding space during the reasoning process. Our analysis shows that both models recover the grid structure during training so that the embeddings corresponding to the points within the grid organize themselves in a 2D subspace and reflect the neighborhood structure of the grid. We also show that the Graph Neural Network we design for the task performs significantly better than the Transformer and is also easier to scale.

Neural Approaches to SAT Solving: Design Choices and Interpretability

In this contribution, we provide a comprehensive evaluation of graph neural networks applied to Boolean satisfiability problems, accompanied by an intuitive explanation of the mechanisms enabling the model to generalize to different instances. We introduce several training improvements, particularly a novel closest assignment supervision method that dynamically adapts to the model's current state, significantly enhancing performance on problems with larger solution spaces. Our experiments demonstrate the suitability of variable-clause graph representations with recurrent neural network updates, which achieve good accuracy on SAT assignment prediction while reducing computational demands. We extend the base graph neural network into a diffusion model that facilitates incremental sampling and can be effectively combined with classical techniques like unit propagation. Through analysis of embedding space patterns and optimization trajectories, we show how these networks implicitly perform a process very similar to continuous relaxations of MaxSAT, offering an interpretable view of their reasoning process. This understanding guides our design choices and explains the ability of recurrent architectures to scale effectively at inference time beyond their training distribution, which we demonstrate with test-time scaling experiments.

Understanding GNNs for Boolean Satisfiability through Approximation Algorithms

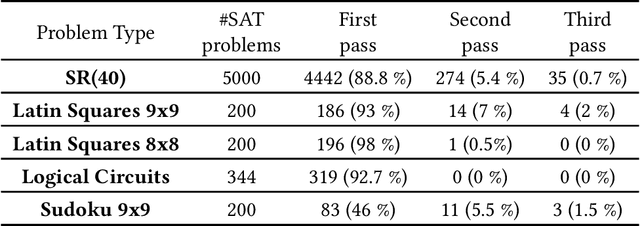
The paper deals with the interpretability of Graph Neural Networks in the context of Boolean Satisfiability. The goal is to demystify the internal workings of these models and provide insightful perspectives into their decision-making processes. This is done by uncovering connections to two approximation algorithms studied in the domain of Boolean Satisfiability: Belief Propagation and Semidefinite Programming Relaxations. Revealing these connections has empowered us to introduce a suite of impactful enhancements. The first significant enhancement is a curriculum training procedure, which incrementally increases the problem complexity in the training set, together with increasing the number of message passing iterations of the Graph Neural Network. We show that the curriculum, together with several other optimizations, reduces the training time by more than an order of magnitude compared to the baseline without the curriculum. Furthermore, we apply decimation and sampling of initial embeddings, which significantly increase the percentage of solved problems.