MizAR 60 for Mizar 50

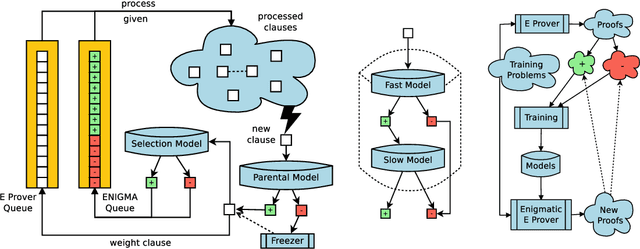
As a present to Mizar on its 50th anniversary, we develop an AI/TP system that automatically proves about 60\% of the Mizar theorems in the hammer setting. We also automatically prove 75\% of the Mizar theorems when the automated provers are helped by using only the premises used in the human-written Mizar proofs. We describe the methods and large-scale experiments leading to these results. This includes in particular the E and Vampire provers, their ENIGMA and Deepire learning modifications, a number of learning-based premise selection methods, and the incremental loop that interleaves growing a corpus of millions of ATP proofs with training increasingly strong AI/TP systems on them. We also present a selection of Mizar problems that were proved automatically.

Planning from Pixels in Environments with Combinatorially Hard Search Spaces

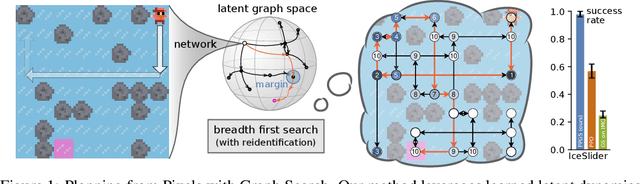
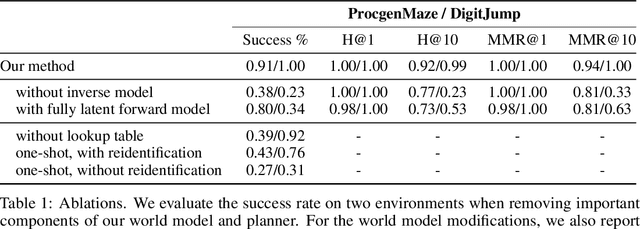
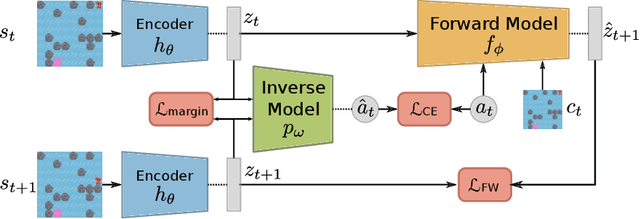
The ability to form complex plans based on raw visual input is a litmus test for current capabilities of artificial intelligence, as it requires a seamless combination of visual processing and abstract algorithmic execution, two traditionally separate areas of computer science. A recent surge of interest in this field brought advances that yield good performance in tasks ranging from arcade games to continuous control; these methods however do not come without significant issues, such as limited generalization capabilities and difficulties when dealing with combinatorially hard planning instances. Our contribution is two-fold: (i) we present a method that learns to represent its environment as a latent graph and leverages state reidentification to reduce the complexity of finding a good policy from exponential to linear (ii) we introduce a set of lightweight environments with an underlying discrete combinatorial structure in which planning is challenging even for humans. Moreover, we show that our methods achieves strong empirical generalization to variations in the environment, even across highly disadvantaged regimes, such as "one-shot" planning, or in an offline RL paradigm which only provides low-quality trajectories.

Reinforcement Learning of Theorem Proving

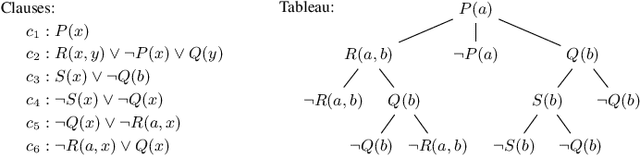
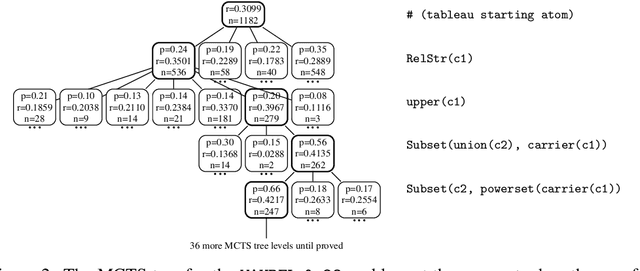
We introduce a theorem proving algorithm that uses practically no domain heuristics for guiding its connection-style proof search. Instead, it runs many Monte-Carlo simulations guided by reinforcement learning from previous proof attempts. We produce several versions of the prover, parameterized by different learning and guiding algorithms. The strongest version of the system is trained on a large corpus of mathematical problems and evaluated on previously unseen problems. The trained system solves within the same number of inferences over 40% more problems than a baseline prover, which is an unusually high improvement in this hard AI domain. To our knowledge this is the first time reinforcement learning has been convincingly applied to solving general mathematical problems on a large scale.