A Simplified and Improved Free-Variable Framework for Hilbert's epsilon as an Operator of Indefinite Committed Choice

Free variables occur frequently in mathematics and computer science with ad hoc and altering semantics. We present the most recent version of our free-variable framework for two-valued logics with properly improved functionality, but only two kinds of free variables left (instead of three): implicitly universally and implicitly existentially quantified ones, now simply called "free atoms" and "free variables", respectively. The quantificational expressiveness and the problem-solving facilities of our framework exceed standard first-order and even higher-order modal logics, and directly support Fermat's descente infinie. With the improved version of our framework, we can now model also Henkin quantification, neither using quantifiers (binders) nor raising (Skolemization). We propose a new semantics for Hilbert's epsilon as a choice operator with the following features: We avoid overspecification (such as right-uniqueness), but admit indefinite choice, committed choice, and classical logics. Moreover, our semantics for the epsilon supports reductive proof search optimally.

The RatioLog Project: Rational Extensions of Logical Reasoning

Higher-level cognition includes logical reasoning and the ability of question answering with common sense. The RatioLog project addresses the problem of rational reasoning in deep question answering by methods from automated deduction and cognitive computing. In a first phase, we combine techniques from information retrieval and machine learning to find appropriate answer candidates from the huge amount of text in the German version of the free encyclopedia "Wikipedia". In a second phase, an automated theorem prover tries to verify the answer candidates on the basis of their logical representations. In a third phase - because the knowledge may be incomplete and inconsistent -, we consider extensions of logical reasoning to improve the results. In this context, we work toward the application of techniques from human reasoning: We employ defeasible reasoning to compare the answers w.r.t. specificity, deontic logic, normative reasoning, and model construction. Moreover, we use integrated case-based reasoning and machine learning techniques on the basis of the semantic structure of the questions and answer candidates to learn giving the right answers.

Automation of Mathematical Induction as part of the History of Logic

We review the history of the automation of mathematical induction

Lectures on Jacques Herbrand as a Logician

We give some lectures on the work on formal logic of Jacques Herbrand, and sketch his life and his influence on automated theorem proving. The intended audience ranges from students interested in logic over historians to logicians. Besides the well-known correction of Herbrand's False Lemma by Goedel and Dreben, we also present the hardly known unpublished correction of Heijenoort and its consequences on Herbrand's Modus Ponens Elimination. Besides Herbrand's Fundamental Theorem and its relation to the Loewenheim-Skolem-Theorem, we carefully investigate Herbrand's notion of intuitionism in connection with his notion of falsehood in an infinite domain. We sketch Herbrand's two proofs of the consistency of arithmetic and his notion of a recursive function, and last but not least, present the correct original text of his unification algorithm with a new translation.

David Poole's Specificity Revised

In the middle of the 1980s, David Poole introduced a semantical, model-theoretic notion of specificity to the artificial-intelligence community. Since then it has found further applications in non-monotonic reasoning, in particular in defeasible reasoning. Poole tried to approximate the intuitive human concept of specificity, which seems to be essential for reasoning in everyday life with its partial and inconsistent information. His notion, however, turns out to be intricate and problematic, which --- as we show --- can be overcome to some extent by a closer approximation of the intuitive human concept of specificity. Besides the intuitive advantages of our novel specificity ordering over Poole's specificity relation in the classical examples of the literature, we also report some hard mathematical facts: Contrary to what was claimed before, we show that Poole's relation is not transitive. The present means to decide our novel specificity relation, however, show only a slight improvement over the known ones for Poole's relation, and further work is needed in this aspect.

Hilbert's epsilon as an Operator of Indefinite Committed Choice

Paul Bernays and David Hilbert carefully avoided overspecification of Hilbert's epsilon-operator and axiomatized only what was relevant for their proof-theoretic investigations. Semantically, this left the epsilon-operator underspecified. In the meanwhile, there have been several suggestions for semantics of the epsilon as a choice operator. After reviewing the literature on semantics of Hilbert's epsilon operator, we propose a new semantics with the following features: We avoid overspecification (such as right-uniqueness), but admit indefinite choice, committed choice, and classical logics. Moreover, our semantics for the epsilon supports proof search optimally and is natural in the sense that it does not only mirror some cases of referential interpretation of indefinite articles in natural language, but may also contribute to philosophy of language. Finally, we ask the question whether our epsilon within our free-variable framework can serve as a paradigm useful in the specification and computation of semantics of discourses in natural language.

A Self-Contained and Easily Accessible Discussion of the Method of Descente Infinie and Fermat's Only Explicitly Known Proof by Descente Infinie

We present the only proof of Pierre Fermat by descente infinie that is known to exist today. As the text of its Latin original requires active mathematical interpretation, it is more a proof sketch than a proper mathematical proof. We discuss descente infinie from the mathematical, logical, historical, linguistic, and refined logic-historical points of view. We provide the required preliminaries from number theory and develop a self-contained proof in a modern form, which nevertheless is intended to follow Fermat's ideas closely. We then annotate an English translation of Fermat's original proof with terms from the modern proof. Including all important facts, we present a concise and self-contained discussion of Fermat's proof sketch, which is easily accessible to laymen in number theory as well as to laymen in the history of mathematics, and which provides new clarification of the Method of Descente Infinie to the experts in these fields. Last but not least, this paper fills a gap regarding the easy accessibility of the subject.

Progress in Computer-Assisted Inductive Theorem Proving by Human-Orientedness and Descente Infinie?

In this short position paper we briefly review the development history of automated inductive theorem proving and computer-assisted mathematical induction. We think that the current low expectations on progress in this field result from a faulty narrow-scope historical projection. Our main motivation is to explain--on an abstract but hopefully sufficiently descriptive level--why we believe that future progress in the field is to result from human-orientedness and descente infinie.

Full First-Order Sequent and Tableau Calculi With Preservation of Solutions and the Liberalized delta-Rule but Without Skolemization

We present a combination of raising, explicit variable dependency representation, the liberalized delta-rule, and preservation of solutions for first-order deductive theorem proving. Our main motivation is to provide the foundation for our work on inductive theorem proving, where the preservation of solutions is indispensable.

An Algebraic Dexter-Based Hypertext Reference Model

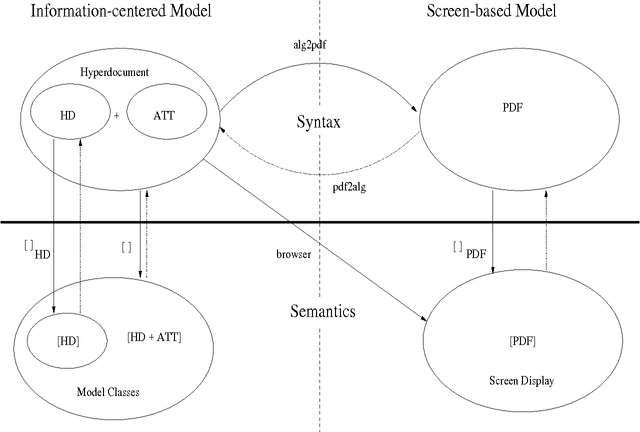
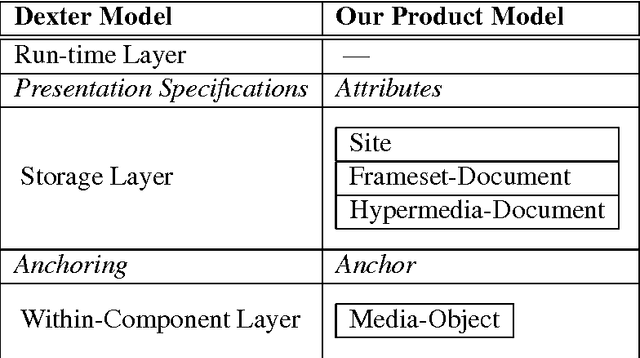
We present the first formal algebraic specification of a hypertext reference model. It is based on the well-known Dexter Hypertext Reference Model and includes modifications with respect to the development of hypertext since the WWW came up. Our hypertext model was developed as a product model with the aim to automatically support the design process and is extended to a model of hypertext-systems in order to be able to describe the state transitions in this process. While the specification should be easy to read for non-experts in algebraic specification, it guarantees a unique understanding and enables a close connection to logic-based development and verification.