Towards an Intelligent Tutor for Mathematical Proofs

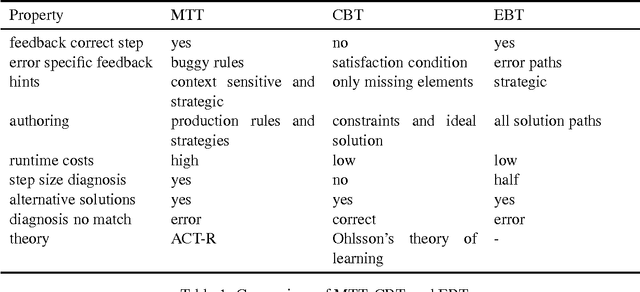
Computer-supported learning is an increasingly important form of study since it allows for independent learning and individualized instruction. In this paper, we discuss a novel approach to developing an intelligent tutoring system for teaching textbook-style mathematical proofs. We characterize the particularities of the domain and discuss common ITS design models. Our approach is motivated by phenomena found in a corpus of tutorial dialogs that were collected in a Wizard-of-Oz experiment. We show how an intelligent tutor for textbook-style mathematical proofs can be built on top of an adapted assertion-level proof assistant by reusing representations and proof search strategies originally developed for automated and interactive theorem proving. The resulting prototype was successfully evaluated on a corpus of tutorial dialogs and yields good results.

Granularity-Adaptive Proof Presentation

When mathematicians present proofs they usually adapt their explanations to their didactic goals and to the (assumed) knowledge of their addressees. Modern automated theorem provers, in contrast, present proofs usually at a fixed level of detail (also called granularity). Often these presentations are neither intended nor suitable for human use. A challenge therefore is to develop user- and goal-adaptive proof presentation techniques that obey common mathematical practice. We present a flexible and adaptive approach to proof presentation that exploits machine learning techniques to extract a model of the specific granularity of proof examples and employs this model for the automated generation of further proofs at an adapted level of granularity.