Patrice Perny
Bayesian preference elicitation for multiobjective combinatorial optimization
Jul 29, 2020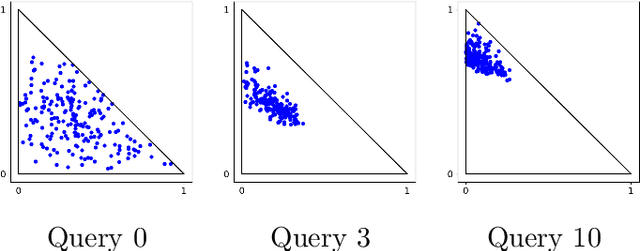

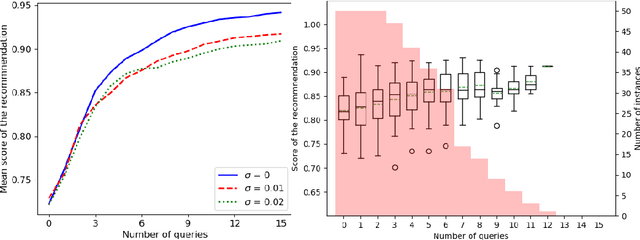
Abstract:We introduce a new incremental preference elicitation procedure able to deal with noisy responses of a Decision Maker (DM). The originality of the contribution is to propose a Bayesian approach for determining a preferred solution in a multiobjective decision problem involving a combinatorial set of alternatives. We assume that the preferences of the DM are represented by an aggregation function whose parameters are unknown and that the uncertainty about them is represented by a density function on the parameter space. Pairwise comparison queries are used to reduce this uncertainty (by Bayesian revision). The query selection strategy is based on the solution of a mixed integer linear program with a combinatorial set of variables and constraints, which requires to use columns and constraints generation methods. Numerical tests are provided to show the practicability of the approach.
Approximation of Lorenz-Optimal Solutions in Multiobjective Markov Decision Processes
Sep 26, 2013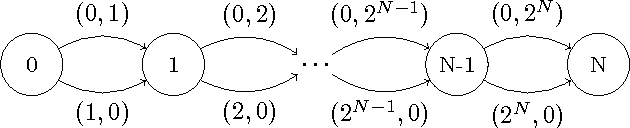
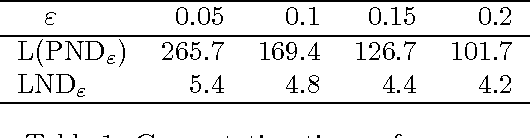
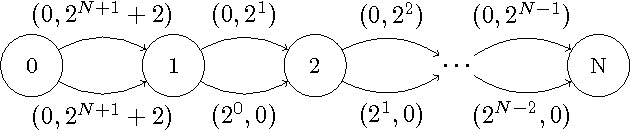
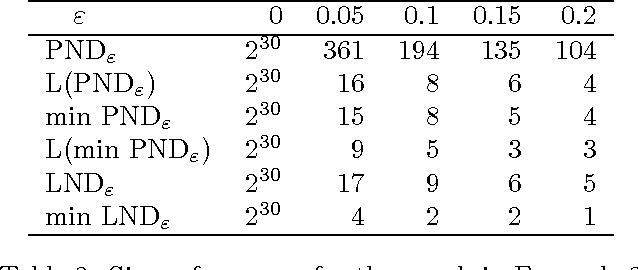
Abstract:This paper is devoted to fair optimization in Multiobjective Markov Decision Processes (MOMDPs). A MOMDP is an extension of the MDP model for planning under uncertainty while trying to optimize several reward functions simultaneously. This applies to multiagent problems when rewards define individual utility functions, or in multicriteria problems when rewards refer to different features. In this setting, we study the determination of policies leading to Lorenz-non-dominated tradeoffs. Lorenz dominance is a refinement of Pareto dominance that was introduced in Social Choice for the measurement of inequalities. In this paper, we introduce methods to efficiently approximate the sets of Lorenz-non-dominated solutions of infinite-horizon, discounted MOMDPs. The approximations are polynomial-sized subsets of those solutions.
Qualitative Models for Decision Under Uncertainty without the Commensurability Assumption
Jan 23, 2013Abstract:This paper investigates a purely qualitative version of Savage's theory for decision making under uncertainty. Until now, most representation theorems for preference over acts rely on a numerical representation of utility and uncertainty where utility and uncertainty are commensurate. Disrupting the tradition, we relax this assumption and introduce a purely ordinal axiom requiring that the Decision Maker (DM) preference between two acts only depends on the relative position of their consequences for each state. Within this qualitative framework, we determine the only possible form of the decision rule and investigate some instances compatible with the transitivity of the strict preference. Finally we propose a mild relaxation of our ordinality axiom, leaving room for a new family of qualitative decision rules compatible with transitivity.
An Axiomatic Approach to Robustness in Search Problems with Multiple Scenarios
Oct 19, 2012

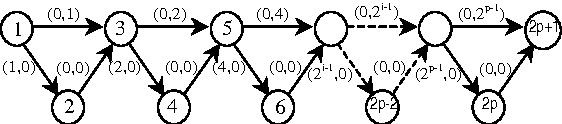
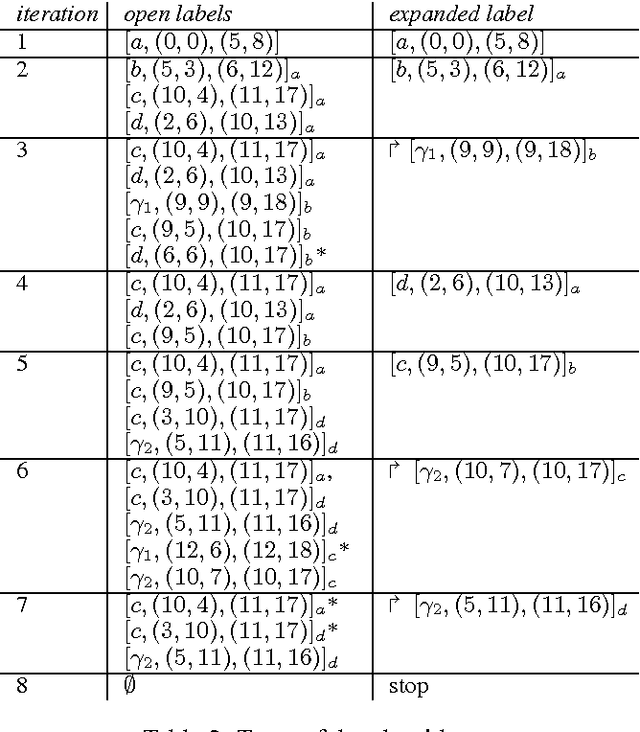
Abstract:This paper is devoted to the search of robust solutions in state space graphs when costs depend on scenarios. We first present axiomatic requirements for preference compatibility with the intuitive idea of robustness.This leads us to propose the Lorenz dominance rule as a basis for robustness analysis. Then, after presenting complexity results about the determination of robust solutions, we propose a new sophistication of A* specially designed to determine the set of robust paths in a state space graph. The behavior of the algorithm is illustrated on a small example. Finally, an axiomatic justification of the refinement of robustness by an OWA criterion is provided.
Search for Choquet-optimal paths under uncertainty
Jun 20, 2012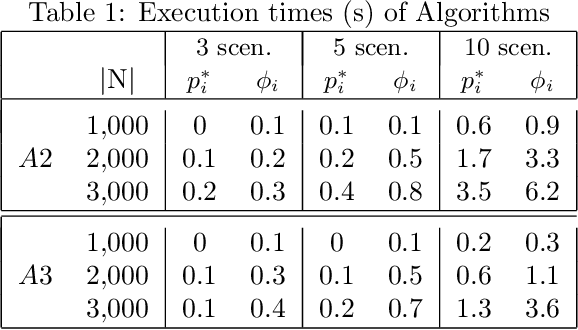
Abstract:Choquet expected utility (CEU) is one of the most sophisticated decision criteria used in decision theory under uncertainty. It provides a generalisation of expected utility enhancing both descriptive and prescriptive possibilities. In this paper, we investigate the use of CEU for path-planning under uncertainty with a special focus on robust solutions. We first recall the main features of the CEU model and introduce some examples showing its descriptive potential. Then we focus on the search for Choquet-optimal paths in multivalued implicit graphs where costs depend on different scenarios. After discussing complexity issues, we propose two different heuristic search algorithms to solve the problem. Finally, numerical experiments are reported, showing the practical efficiency of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge