Robust Ordinal Regression for Subsets Comparisons with Interactions

This paper is dedicated to a robust ordinal method for learning the preferences of a decision maker between subsets. The decision model, derived from Fishburn and LaValle (1996) and whose parameters we learn, is general enough to be compatible with any strict weak order on subsets, thanks to the consideration of possible interactions between elements. Moreover, we accept not to predict some preferences if the available preference data are not compatible with a reliable prediction. A predicted preference is considered reliable if all the simplest models (Occam's razor) explaining the preference data agree on it. Following the robust ordinal regression methodology, our predictions are based on an uncertainty set encompassing the possible values of the model parameters. We define a robust ordinal dominance relation between subsets and we design a procedure to determine whether this dominance relation holds. Numerical tests are provided on synthetic and real-world data to evaluate the richness and reliability of the preference predictions made.

Cautious Learning of Multiattribute Preferences

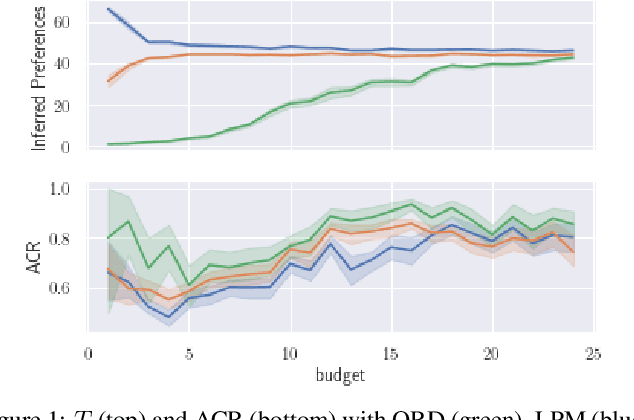
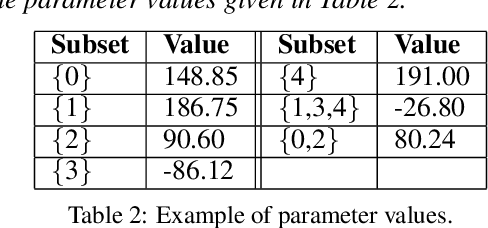
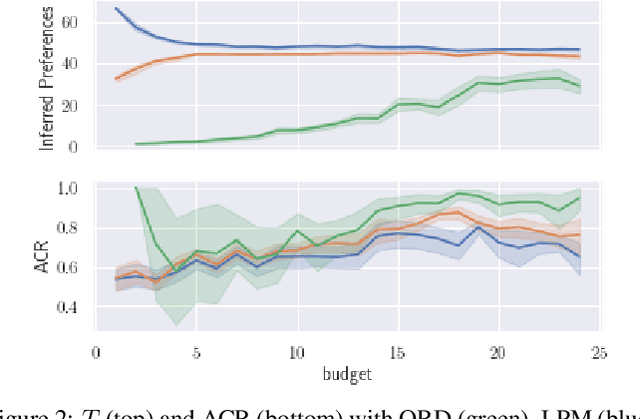
This paper is dedicated to a cautious learning methodology for predicting preferences between alternatives characterized by binary attributes (formally, each alternative is seen as a subset of attributes). By "cautious", we mean that the model learned to represent the multi-attribute preferences is general enough to be compatible with any strict weak order on the alternatives, and that we allow ourselves not to predict some preferences if the data collected are not compatible with a reliable prediction. A predicted preference will be considered reliable if all the simplest models (following Occam's razor principle) explaining the training data agree on it. Predictions are based on an ordinal dominance relation between alternatives [Fishburn and LaValle, 1996]. The dominance relation relies on an uncertainty set encompassing the possible values of the parameters of the multi-attribute utility function. Numerical tests are provided to evaluate the richness and the reliability of the predictions made.

Kemeny ranking is NP-hard for 2-dimensional Euclidean preferences

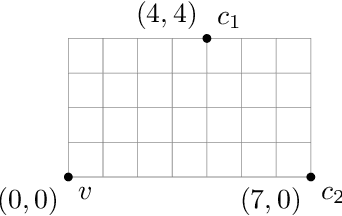
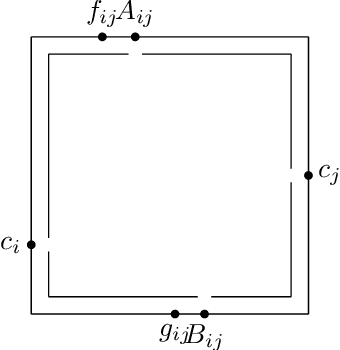
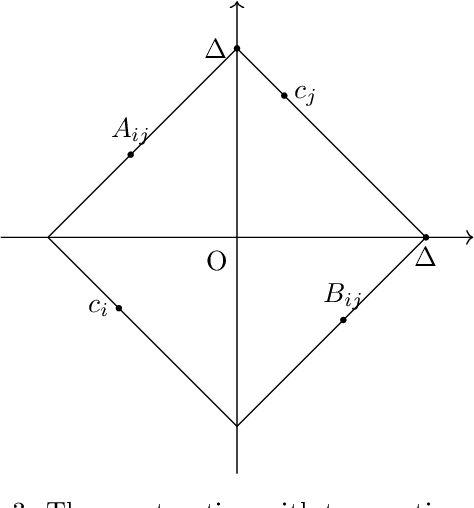
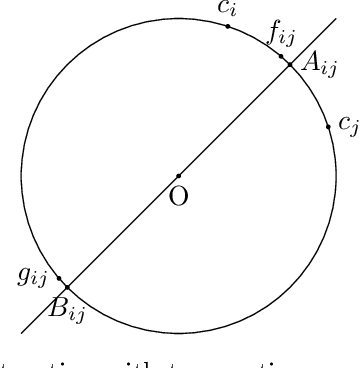
The assumption that voters' preferences share some common structure is a standard way to circumvent NP-hardness results in social choice problems. While the Kemeny ranking problem is NP-hard in the general case, it is known to become easy if the preferences are 1-dimensional Euclidean. In this note, we prove that the Kemeny ranking problem is NP-hard for d-dimensional Euclidean preferences with d>=2. We note that this result also holds for the Slater ranking problem.

Bayesian preference elicitation for multiobjective combinatorial optimization

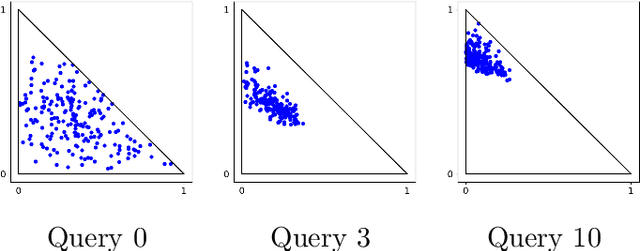
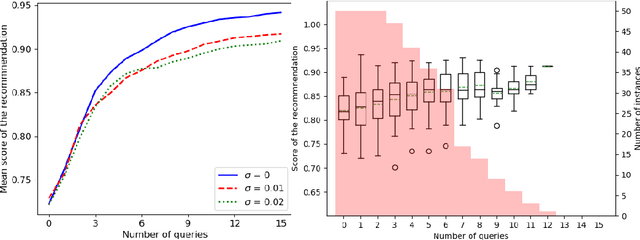
We introduce a new incremental preference elicitation procedure able to deal with noisy responses of a Decision Maker (DM). The originality of the contribution is to propose a Bayesian approach for determining a preferred solution in a multiobjective decision problem involving a combinatorial set of alternatives. We assume that the preferences of the DM are represented by an aggregation function whose parameters are unknown and that the uncertainty about them is represented by a density function on the parameter space. Pairwise comparison queries are used to reduce this uncertainty (by Bayesian revision). The query selection strategy is based on the solution of a mixed integer linear program with a combinatorial set of variables and constraints, which requires to use columns and constraints generation methods. Numerical tests are provided to show the practicability of the approach.

Beyond Pairwise Comparisons in Social Choice: A Setwise Kemeny Aggregation Problem

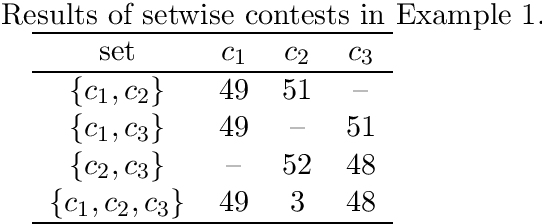
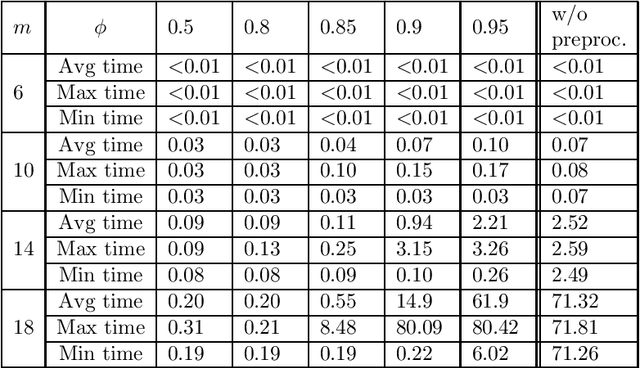
In this paper, we advocate the use of setwise contests for aggregating a set of input rankings into an output ranking. We propose a generalization of the Kemeny rule where one minimizes the number of k-wise disagreements instead of pairwise disagreements (one counts 1 disagreement each time the top choice in a subset of alternatives of cardinality at most k differs between an input ranking and the output ranking). After an algorithmic study of this k-wise Kemeny aggregation problem, we introduce a k-wise counterpart of the majority graph. It reveals useful to divide the aggregation problem into several sub-problems. We conclude with numerical tests.

An Axiomatic Approach to Robustness in Search Problems with Multiple Scenarios

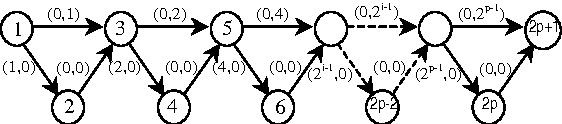
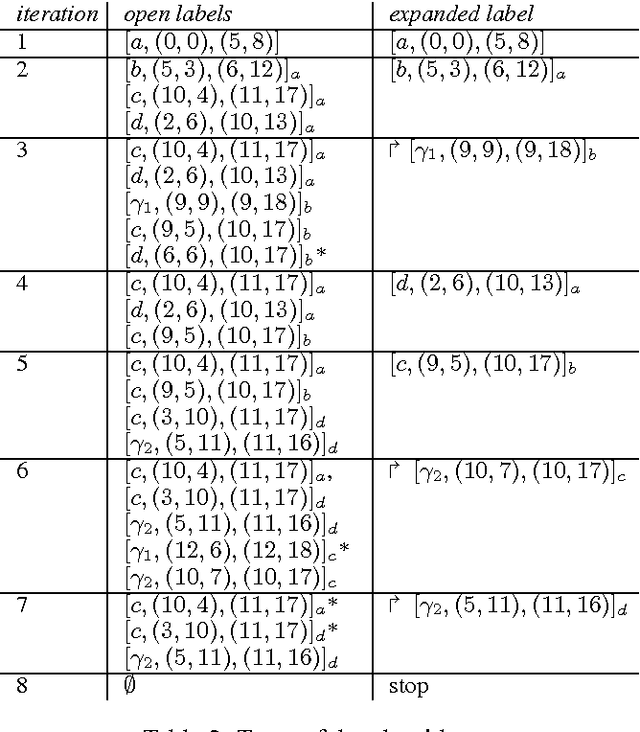
This paper is devoted to the search of robust solutions in state space graphs when costs depend on scenarios. We first present axiomatic requirements for preference compatibility with the intuitive idea of robustness.This leads us to propose the Lorenz dominance rule as a basis for robustness analysis. Then, after presenting complexity results about the determination of robust solutions, we propose a new sophistication of A* specially designed to determine the set of robust paths in a state space graph. The behavior of the algorithm is illustrated on a small example. Finally, an axiomatic justification of the refinement of robustness by an OWA criterion is provided.