Robust Ordinal Regression for Subsets Comparisons with Interactions

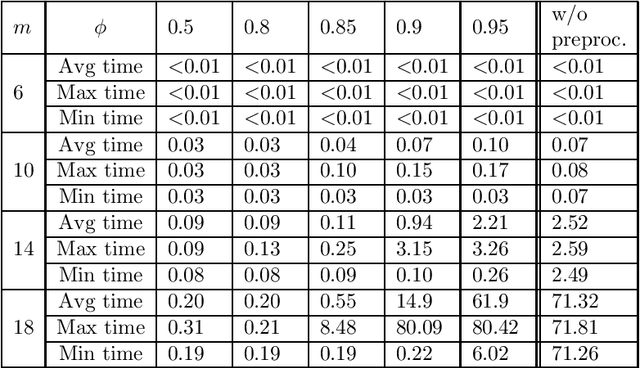
This paper is dedicated to a robust ordinal method for learning the preferences of a decision maker between subsets. The decision model, derived from Fishburn and LaValle (1996) and whose parameters we learn, is general enough to be compatible with any strict weak order on subsets, thanks to the consideration of possible interactions between elements. Moreover, we accept not to predict some preferences if the available preference data are not compatible with a reliable prediction. A predicted preference is considered reliable if all the simplest models (Occam's razor) explaining the preference data agree on it. Following the robust ordinal regression methodology, our predictions are based on an uncertainty set encompassing the possible values of the model parameters. We define a robust ordinal dominance relation between subsets and we design a procedure to determine whether this dominance relation holds. Numerical tests are provided on synthetic and real-world data to evaluate the richness and reliability of the preference predictions made.

Measuring a Priori Voting Power -- Taking Delegations Seriously

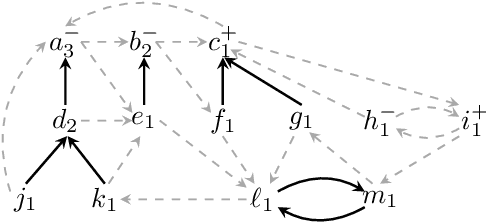
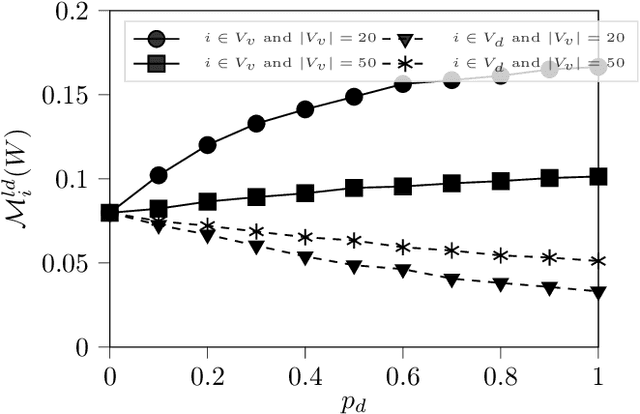
In this paper, we introduce new power indices to measure the criticality of voters involved in different elections where delegations play a key role, namely, two variants of the proxy voting setting and a liquid democracy setting. First, we argue that our power indices are natural extensions of the Penrose-Banzhaf index in classic simple voting games, illustrating their intuitions. We show that recursive formulas can compute these indices for weighted voting games in pseudo-polynomial time. Last, we highlight theoretical properties and provide numerical results to illustrate how introducing delegation options modifies the voting power of voters.

Thou Shalt not Pick all Items if Thou are First: of Strategyproof and Fair Picking Sequences

When allocating indivisible items to agents, it is known that the only strategyproof mechanisms that satisfy a set of rather mild conditions are constrained serial dictatorships: given a fixed order over agents, at each step the designated agent chooses a given number of items (depending on her position in the sequence). With these rules, also known as non-interleaving picking sequences, agents who come earlier in the sequence have a larger choice of items. However, this advantage can be compensated by a higher number of items received by those who come later. How to balance priority in the sequence and number of items received is a nontrivial question. We use a previous model, parameterized by a mapping from ranks to scores, a social welfare functional, and a distribution over preference profiles. For several meaningful choices of parameters, we show that the optimal sequence can be computed in polynomial time. Last, we give a simple procedure for eliciting scoring vectors and we study the impact of the assignment from agents to positions on the ex-post social welfare.

Cautious Learning of Multiattribute Preferences

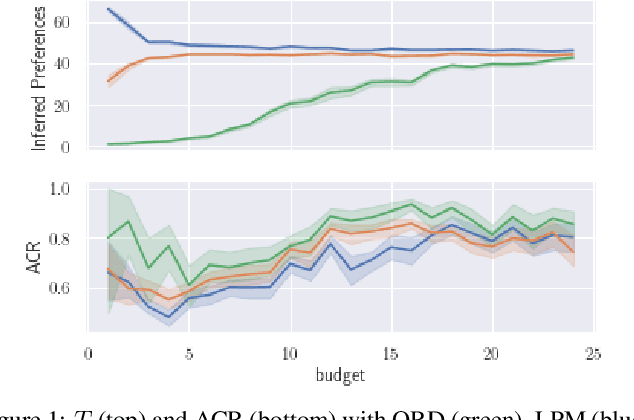
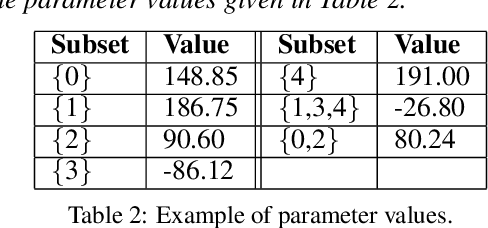
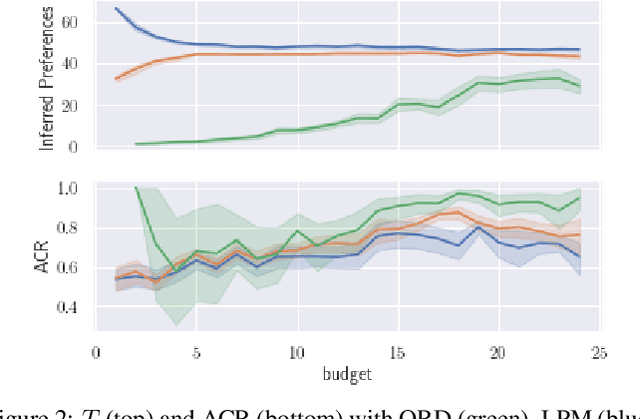
This paper is dedicated to a cautious learning methodology for predicting preferences between alternatives characterized by binary attributes (formally, each alternative is seen as a subset of attributes). By "cautious", we mean that the model learned to represent the multi-attribute preferences is general enough to be compatible with any strict weak order on the alternatives, and that we allow ourselves not to predict some preferences if the data collected are not compatible with a reliable prediction. A predicted preference will be considered reliable if all the simplest models (following Occam's razor principle) explaining the training data agree on it. Predictions are based on an ordinal dominance relation between alternatives [Fishburn and LaValle, 1996]. The dominance relation relies on an uncertainty set encompassing the possible values of the parameters of the multi-attribute utility function. Numerical tests are provided to evaluate the richness and the reliability of the predictions made.

Computation and Bribery of Voting Power in Delegative Simple Games

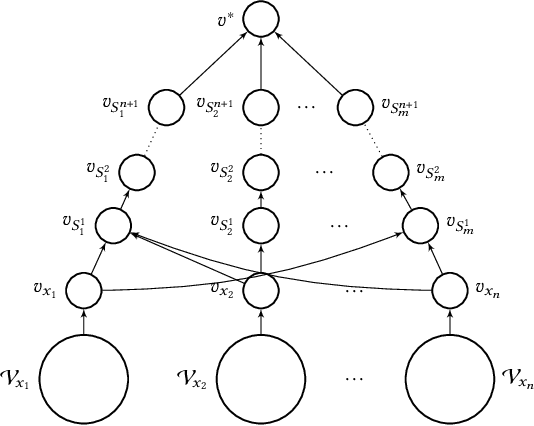
Weighted voting games is one of the most important classes of cooperative games. Recently, Zhang and Grossi [53] proposed a variant of this class, called delegative simple games, which is well suited to analyse the relative importance of each voter in liquid democracy elections. Moreover, they defined a power index, called the delagative Banzhaf index to compute the importance of each agent (i.e., both voters and delegators) in a delegation graph based on two key parameters: the total voting weight she has accumulated and the structure of supports she receives from her delegators. We obtain several results related to delegative simple games. We first propose a pseudo-polynomial time algorithm to compute the delegative Banzhaf and Shapley-Shubik values in delegative simple games. We then investigate a bribery problem where the goal is to maximize/minimize the voting power/weight of a given voter in a delegation graph by changing at most a fixed number of delegations. We show that the problems of minimizing/maximizing a voter's power index value are strongly NP-hard. Furthermore, we prove that having a better approximation guarantee than $1-1/e$ to maximize the voting weight of a voter is not possible, unless $P = NP$, then we provide some parameterized complexity results for this problem. Finally, we show that finding a delegation graph with a given number of gurus that maximizes the minimum power index value an agent can have is a computationally hard problem.

When Can Liquid Democracy Unveil the Truth?

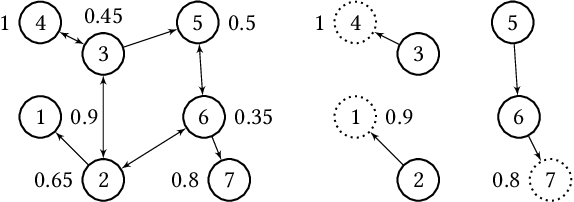
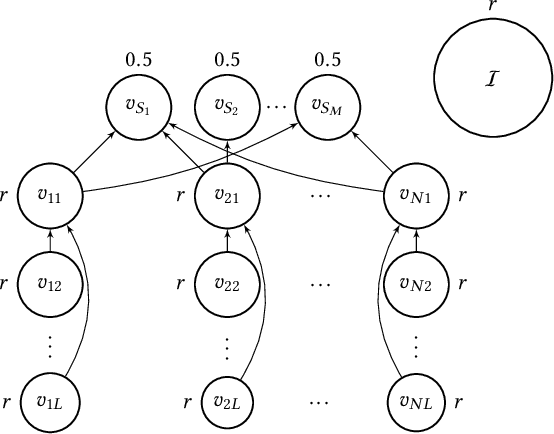
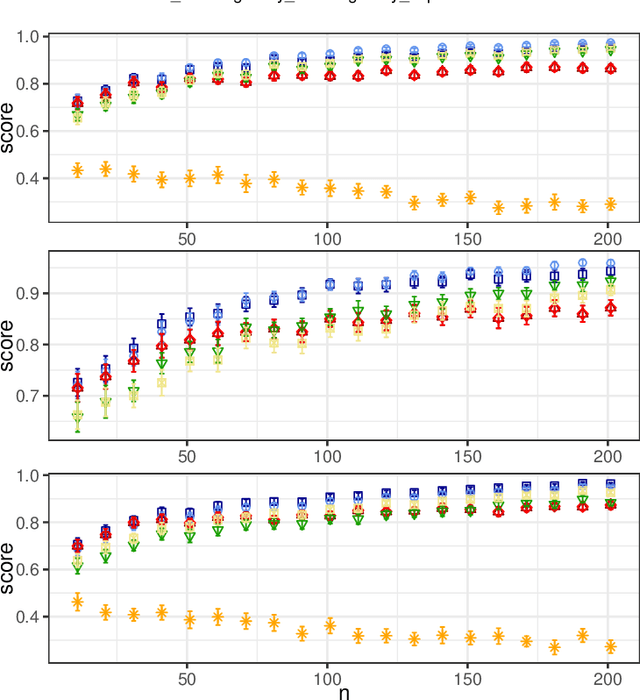
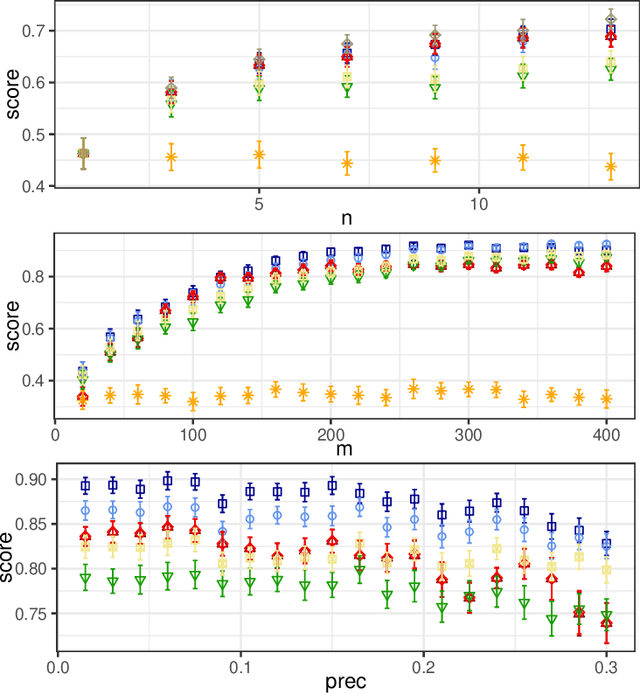
In this paper, we investigate the so-called ODP-problem that has been formulated by Caragiannis and Micha [10]. Here, we are in a setting with two election alternatives out of which one is assumed to be correct. In ODP, the goal is to organise the delegations in the social network in order to maximize the probability that the correct alternative, referred to as ground truth, is elected. While the problem is known to be computationally hard, we strengthen existing hardness results by providing a novel strong approximation hardness result: For any positive constant $C$, we prove that, unless $P=NP$, there is no polynomial-time algorithm for ODP that achieves an approximation guarantee of $\alpha \ge (\ln n)^{-C}$, where $n$ is the number of voters. The reduction designed for this result uses poorly connected social networks in which some voters suffer from misinformation. Interestingly, under some hypothesis on either the accuracies of voters or the connectivity of the network, we obtain a polynomial-time $1/2$-approximation algorithm. This observation proves formally that the connectivity of the social network is a key feature for the efficiency of the liquid democracy paradigm. Lastly, we run extensive simulations and observe that simple algorithms (working either in a centralized or decentralized way) outperform direct democracy on a large class of instances. Overall, our contributions yield new insights on the question in which situations liquid democracy can be beneficial.

Beyond Pairwise Comparisons in Social Choice: A Setwise Kemeny Aggregation Problem

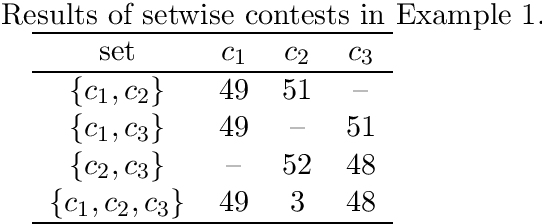
In this paper, we advocate the use of setwise contests for aggregating a set of input rankings into an output ranking. We propose a generalization of the Kemeny rule where one minimizes the number of k-wise disagreements instead of pairwise disagreements (one counts 1 disagreement each time the top choice in a subset of alternatives of cardinality at most k differs between an input ranking and the output ranking). After an algorithmic study of this k-wise Kemeny aggregation problem, we introduce a k-wise counterpart of the majority graph. It reveals useful to divide the aggregation problem into several sub-problems. We conclude with numerical tests.

The Convergence of Iterative Delegations in Liquid Democracy in a Social Network

Liquid democracy is a collective decision making paradigm which lies between direct and representative democracy. One of its main features is that voters can delegate their votes in a transitive manner such that: A delegates to B and B delegates to C leads to A indirectly delegates to C. These delegations can be effectively empowered by implementing liquid democracy in a social network, so that voters can delegate their votes to any of their neighbors in the network. However, it is uncertain that such a delegation process will lead to a stable state where all voters are satisfied with the people representing them. We study the stability (w.r.t. voters preferences) of the delegation process in liquid democracy and model it as a game in which the players are the voters and the strategies are their possible delegations. We answer several questions on the equilibria of this process in any social network or in social networks that correspond to restricted types of graphs. We show that a Nash-equilibrium may not exist, and that it is even NP-complete to decide whether one exists or not. This holds even if the social network is a complete graph or a bounded degree graph. We further show that this existence problem is W[1]-hard w.r.t. the treewidth of the social network. Besides these hardness results, we demonstrate that an equilibrium always exists whatever the preferences of the voters iff the social network is a tree. We design a dynamic programming procedure to determine some desirable equilibria (e.g., minimizing the dissatisfaction of the voters) in polynomial time for tree social networks. Lastly, we study the convergence of delegation dynamics. Unfortunately, when an equilibrium exists, we show that a best response dynamics may not converge, even if the social network is a path or a complete graph.

The Convergence of Iterative Delegations in Liquid Democracy

In this paper, we study liquid democracy, a collective decision making paradigm which lies between direct and representative democracy. One main feature of liquid democracy is that voters can delegate their votes in a transitive manner such that: A delegates to B and B delegates to C leads to A delegates to C. We study the stability (w.r.t. voters preferences) of the delegation process in liquid democracy and model it as a game in which the players are the voters and the strategies are possible delegations. This game-theoretic model enables us to answer several questions on the equilibria of this process under general preferences and several types of restricted preferences (e.g., single-peaked preferences).

Optimizing Quantiles in Preference-based Markov Decision Processes

In the Markov decision process model, policies are usually evaluated by expected cumulative rewards. As this decision criterion is not always suitable, we propose in this paper an algorithm for computing a policy optimal for the quantile criterion. Both finite and infinite horizons are considered. Finally we experimentally evaluate our approach on random MDPs and on a data center control problem.