Ruben Becker
When Can Liquid Democracy Unveil the Truth?
Apr 05, 2021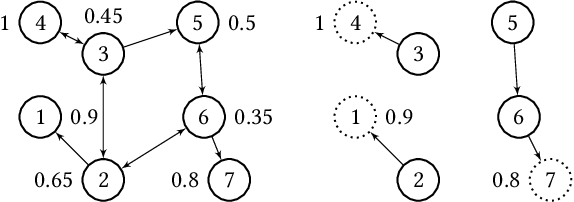
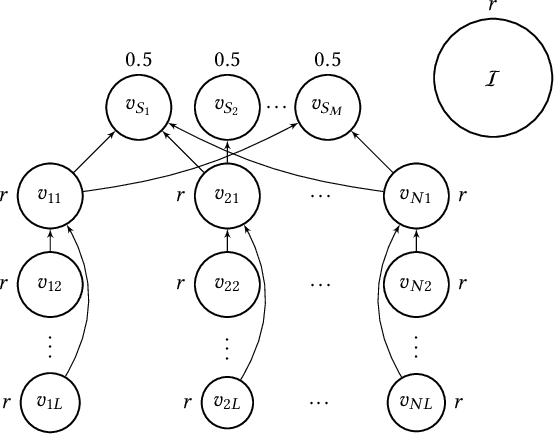
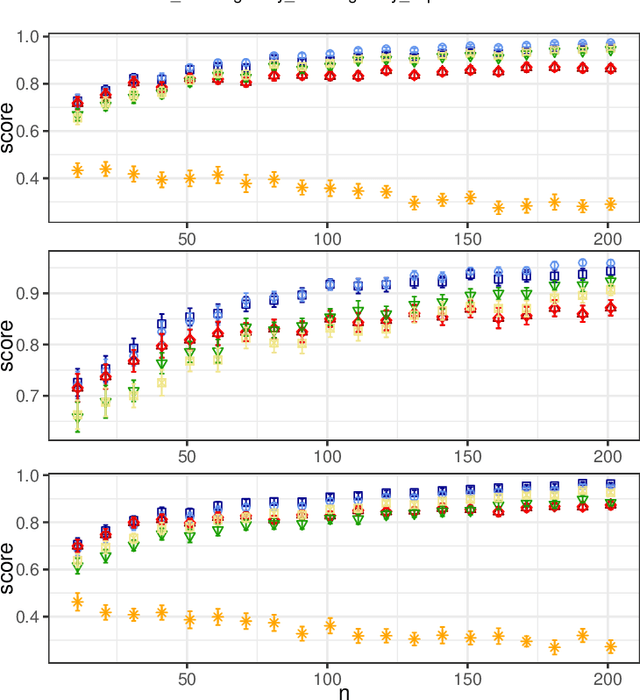
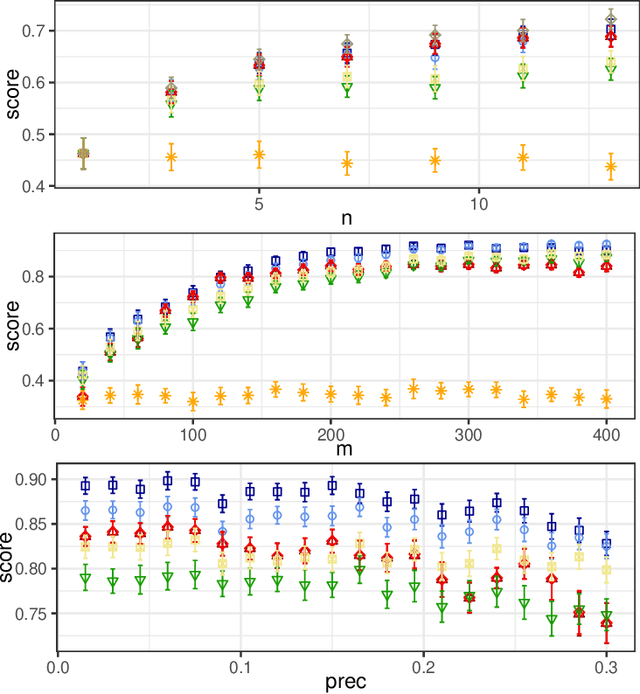
Abstract:In this paper, we investigate the so-called ODP-problem that has been formulated by Caragiannis and Micha [10]. Here, we are in a setting with two election alternatives out of which one is assumed to be correct. In ODP, the goal is to organise the delegations in the social network in order to maximize the probability that the correct alternative, referred to as ground truth, is elected. While the problem is known to be computationally hard, we strengthen existing hardness results by providing a novel strong approximation hardness result: For any positive constant $C$, we prove that, unless $P=NP$, there is no polynomial-time algorithm for ODP that achieves an approximation guarantee of $\alpha \ge (\ln n)^{-C}$, where $n$ is the number of voters. The reduction designed for this result uses poorly connected social networks in which some voters suffer from misinformation. Interestingly, under some hypothesis on either the accuracies of voters or the connectivity of the network, we obtain a polynomial-time $1/2$-approximation algorithm. This observation proves formally that the connectivity of the social network is a key feature for the efficiency of the liquid democracy paradigm. Lastly, we run extensive simulations and observe that simple algorithms (working either in a centralized or decentralized way) outperform direct democracy on a large class of instances. Overall, our contributions yield new insights on the question in which situations liquid democracy can be beneficial.
Subspace Determination through Local Intrinsic Dimensional Decomposition: Theory and Experimentation
Jul 15, 2019
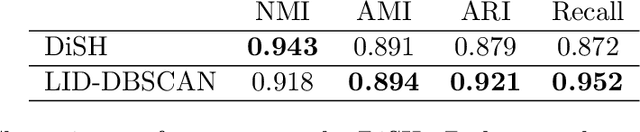

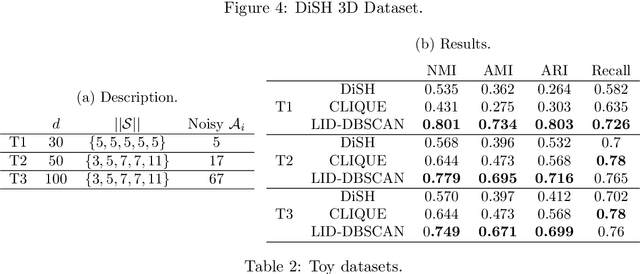
Abstract:Axis-aligned subspace clustering generally entails searching through enormous numbers of subspaces (feature combinations) and evaluation of cluster quality within each subspace. In this paper, we tackle the problem of identifying subsets of features with the most significant contribution to the formation of the local neighborhood surrounding a given data point. For each point, the recently-proposed Local Intrinsic Dimension (LID) model is used in identifying the axis directions along which features have the greatest local discriminability, or equivalently, the fewest number of components of LID that capture the local complexity of the data. In this paper, we develop an estimator of LID along axis projections, and provide preliminary evidence that this LID decomposition can indicate axis-aligned data subspaces that support the formation of clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge