LDReg: Local Dimensionality Regularized Self-Supervised Learning

Representations learned via self-supervised learning (SSL) can be susceptible to dimensional collapse, where the learned representation subspace is of extremely low dimensionality and thus fails to represent the full data distribution and modalities. Dimensional collapse also known as the "underfilling" phenomenon is one of the major causes of degraded performance on downstream tasks. Previous work has investigated the dimensional collapse problem of SSL at a global level. In this paper, we demonstrate that representations can span over high dimensional space globally, but collapse locally. To address this, we propose a method called $\textit{local dimensionality regularization (LDReg)}$. Our formulation is based on the derivation of the Fisher-Rao metric to compare and optimize local distance distributions at an asymptotically small radius for each data point. By increasing the local intrinsic dimensionality, we demonstrate through a range of experiments that LDReg improves the representation quality of SSL. The results also show that LDReg can regularize dimensionality at both local and global levels.

Dimensionality-Aware Outlier Detection: Theoretical and Experimental Analysis

We present a nonparametric method for outlier detection that takes full account of local variations in intrinsic dimensionality within the dataset. Using the theory of Local Intrinsic Dimensionality (LID), our 'dimensionality-aware' outlier detection method, DAO, is derived as an estimator of an asymptotic local expected density ratio involving the query point and a close neighbor drawn at random. The dimensionality-aware behavior of DAO is due to its use of local estimation of LID values in a theoretically-justified way. Through comprehensive experimentation on more than 800 synthetic and real datasets, we show that DAO significantly outperforms three popular and important benchmark outlier detection methods: Local Outlier Factor (LOF), Simplified LOF, and kNN.

Intrinsic Dimensionality Estimation within Tight Localities: A Theoretical and Experimental Analysis

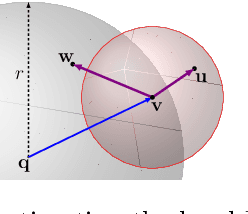
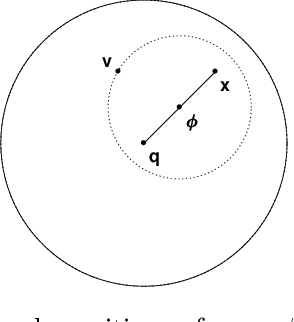
Accurate estimation of Intrinsic Dimensionality (ID) is of crucial importance in many data mining and machine learning tasks, including dimensionality reduction, outlier detection, similarity search and subspace clustering. However, since their convergence generally requires sample sizes (that is, neighborhood sizes) on the order of hundreds of points, existing ID estimation methods may have only limited usefulness for applications in which the data consists of many natural groups of small size. In this paper, we propose a local ID estimation strategy stable even for `tight' localities consisting of as few as 20 sample points. The estimator applies MLE techniques over all available pairwise distances among the members of the sample, based on a recent extreme-value-theoretic model of intrinsic dimensionality, the Local Intrinsic Dimension (LID). Our experimental results show that our proposed estimation technique can achieve notably smaller variance, while maintaining comparable levels of bias, at much smaller sample sizes than state-of-the-art estimators.

Subspace Determination through Local Intrinsic Dimensional Decomposition: Theory and Experimentation

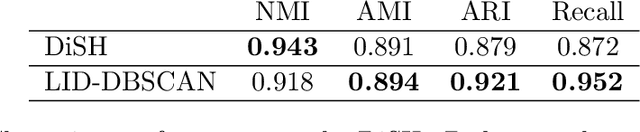
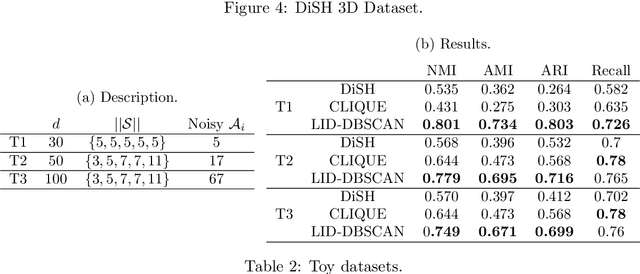
Axis-aligned subspace clustering generally entails searching through enormous numbers of subspaces (feature combinations) and evaluation of cluster quality within each subspace. In this paper, we tackle the problem of identifying subsets of features with the most significant contribution to the formation of the local neighborhood surrounding a given data point. For each point, the recently-proposed Local Intrinsic Dimension (LID) model is used in identifying the axis directions along which features have the greatest local discriminability, or equivalently, the fewest number of components of LID that capture the local complexity of the data. In this paper, we develop an estimator of LID along axis projections, and provide preliminary evidence that this LID decomposition can indicate axis-aligned data subspaces that support the formation of clusters.

Quality Evaluation of GANs Using Cross Local Intrinsic Dimensionality

Generative Adversarial Networks (GANs) are an elegant mechanism for data generation. However, a key challenge when using GANs is how to best measure their ability to generate realistic data. In this paper, we demonstrate that an intrinsic dimensional characterization of the data space learned by a GAN model leads to an effective evaluation metric for GAN quality. In particular, we propose a new evaluation measure, CrossLID, that assesses the local intrinsic dimensionality (LID) of real-world data with respect to neighborhoods found in GAN-generated samples. Intuitively, CrossLID measures the degree to which manifolds of two data distributions coincide with each other. In experiments on 4 benchmark image datasets, we compare our proposed measure to several state-of-the-art evaluation metrics. Our experiments show that CrossLID is strongly correlated with the progress of GAN training, is sensitive to mode collapse, is robust to small-scale noise and image transformations, and robust to sample size. Furthermore, we show how CrossLID can be used within the GAN training process to improve generation quality.

Dimensionality-Driven Learning with Noisy Labels

Datasets with significant proportions of noisy (incorrect) class labels present challenges for training accurate Deep Neural Networks (DNNs). We propose a new perspective for understanding DNN generalization for such datasets, by investigating the dimensionality of the deep representation subspace of training samples. We show that from a dimensionality perspective, DNNs exhibit quite distinctive learning styles when trained with clean labels versus when trained with a proportion of noisy labels. Based on this finding, we develop a new dimensionality-driven learning strategy, which monitors the dimensionality of subspaces during training and adapts the loss function accordingly. We empirically demonstrate that our approach is highly tolerant to significant proportions of noisy labels, and can effectively learn low-dimensional local subspaces that capture the data distribution.

Characterizing Adversarial Subspaces Using Local Intrinsic Dimensionality

Deep Neural Networks (DNNs) have recently been shown to be vulnerable against adversarial examples, which are carefully crafted instances that can mislead DNNs to make errors during prediction. To better understand such attacks, a characterization is needed of the properties of regions (the so-called 'adversarial subspaces') in which adversarial examples lie. We tackle this challenge by characterizing the dimensional properties of adversarial regions, via the use of Local Intrinsic Dimensionality (LID). LID assesses the space-filling capability of the region surrounding a reference example, based on the distance distribution of the example to its neighbors. We first provide explanations about how adversarial perturbation can affect the LID characteristic of adversarial regions, and then show empirically that LID characteristics can facilitate the distinction of adversarial examples generated using state-of-the-art attacks. As a proof-of-concept, we show that a potential application of LID is to distinguish adversarial examples, and the preliminary results show that it can outperform several state-of-the-art detection measures by large margins for five attack strategies considered in this paper across three benchmark datasets. Our analysis of the LID characteristic for adversarial regions not only motivates new directions of effective adversarial defense, but also opens up more challenges for developing new attacks to better understand the vulnerabilities of DNNs.