Local Intrinsic Dimensionality for Dynamic Graph Embeddings

The notion of local intrinsic dimensionality (LID) has important theoretical implications and practical applications in the fields of data mining and machine learning. Recent research efforts indicate that LID measures defined for graphs can improve graph representational learning methods based on random walks. In this paper, we discuss how NC-LID, a LID measure designed for static graphs, can be adapted for dynamic networks. Focusing on dynnode2vec as the most representative dynamic graph embedding method based on random walks, we examine correlations between NC-LID and the intrinsic quality of 10 real-world dynamic network embeddings. The obtained results show that NC-LID can be used as a good indicator of nodes whose embedding vectors do not tend to preserve temporal graph structure well. Thus, our empirical findings constitute the first step towards LID-aware dynamic graph embedding methods.

Dimensionality-Aware Outlier Detection: Theoretical and Experimental Analysis

We present a nonparametric method for outlier detection that takes full account of local variations in intrinsic dimensionality within the dataset. Using the theory of Local Intrinsic Dimensionality (LID), our 'dimensionality-aware' outlier detection method, DAO, is derived as an estimator of an asymptotic local expected density ratio involving the query point and a close neighbor drawn at random. The dimensionality-aware behavior of DAO is due to its use of local estimation of LID values in a theoretically-justified way. Through comprehensive experimentation on more than 800 synthetic and real datasets, we show that DAO significantly outperforms three popular and important benchmark outlier detection methods: Local Outlier Factor (LOF), Simplified LOF, and kNN.

Machine Learning Methods for Device Identification Using Wireless Fingerprinting

Industrial Internet of Things (IoT) systems increasingly rely on wireless communication standards. In a common industrial scenario, indoor wireless IoT devices communicate with access points to deliver data collected from industrial sensors, robots and factory machines. Due to static or quasi-static locations of IoT devices and access points, historical observations of IoT device channel conditions provide a possibility to precisely identify the device without observing its traditional identifiers (e.g., MAC or IP address). Such device identification methods based on wireless fingerprinting gained increased attention lately as an additional cyber-security mechanism for critical IoT infrastructures. In this paper, we perform a systematic study of a large class of machine learning algorithms for device identification using wireless fingerprints for the most popular cellular and Wi-Fi IoT technologies. We design, implement, deploy, collect relevant data sets, train and test a multitude of machine learning algorithms, as a part of the complete end-to-end solution design for device identification via wireless fingerprinting. The proposed solution is currently being deployed in a real-world industrial IoT environment as part of H2020 project COLLABS.

Intrinsic Dimensionality Estimation within Tight Localities: A Theoretical and Experimental Analysis

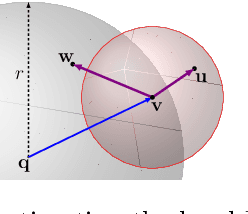
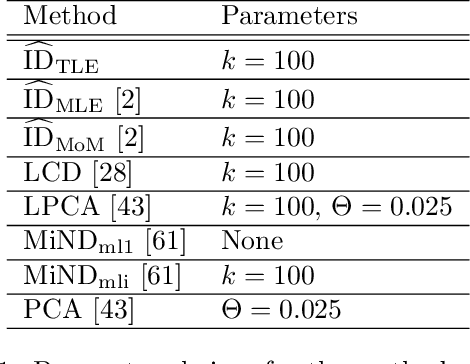
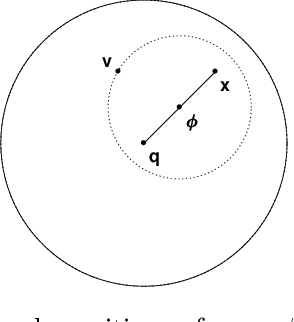
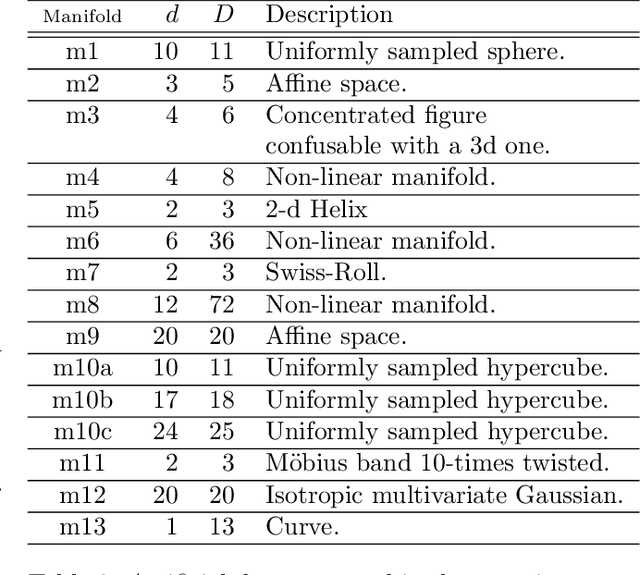
Accurate estimation of Intrinsic Dimensionality (ID) is of crucial importance in many data mining and machine learning tasks, including dimensionality reduction, outlier detection, similarity search and subspace clustering. However, since their convergence generally requires sample sizes (that is, neighborhood sizes) on the order of hundreds of points, existing ID estimation methods may have only limited usefulness for applications in which the data consists of many natural groups of small size. In this paper, we propose a local ID estimation strategy stable even for `tight' localities consisting of as few as 20 sample points. The estimator applies MLE techniques over all available pairwise distances among the members of the sample, based on a recent extreme-value-theoretic model of intrinsic dimensionality, the Local Intrinsic Dimension (LID). Our experimental results show that our proposed estimation technique can achieve notably smaller variance, while maintaining comparable levels of bias, at much smaller sample sizes than state-of-the-art estimators.

Hub-aware Random Walk Graph Embedding Methods for Classification

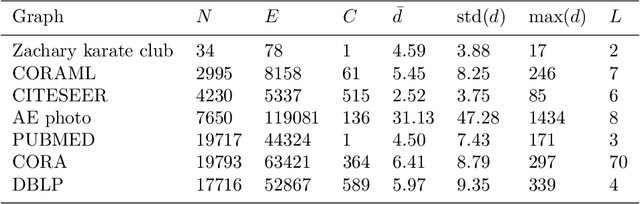
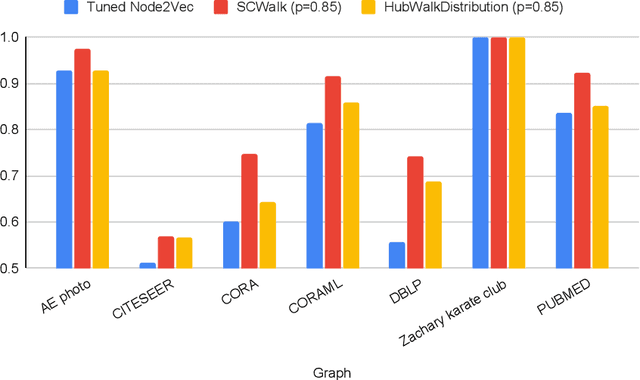
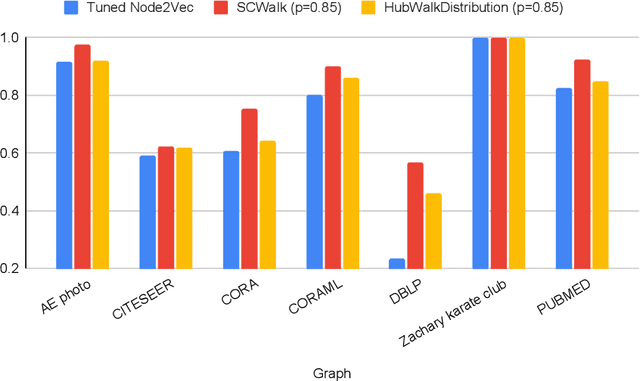
In the last two decades we are witnessing a huge increase of valuable big data structured in the form of graphs or networks. To apply traditional machine learning and data analytic techniques to such data it is necessary to transform graphs into vector-based representations that preserve the most essential structural properties of graphs. For this purpose, a large number of graph embedding methods have been proposed in the literature. Most of them produce general-purpose embeddings suitable for a variety of applications such as node clustering, node classification, graph visualisation and link prediction. In this paper, we propose two novel graph embedding algorithms based on random walks that are specifically designed for the node classification problem. Random walk sampling strategies of the proposed algorithms have been designed to pay special attention to hubs -- high-degree nodes that have the most critical role for the overall connectedness in large-scale graphs. The proposed methods are experimentally evaluated by analyzing the classification performance of three classification algorithms trained on embeddings of real-world networks. The obtained results indicate that our methods considerably improve the predictive power of examined classifiers compared to currently the most popular random walk method for generating general-purpose graph embeddings (node2vec).

Local Intrinsic Dimensionality Measures for Graphs, with Applications to Graph Embeddings

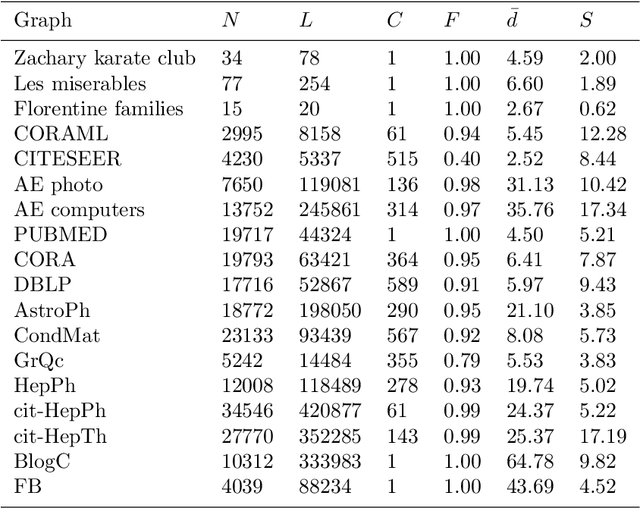
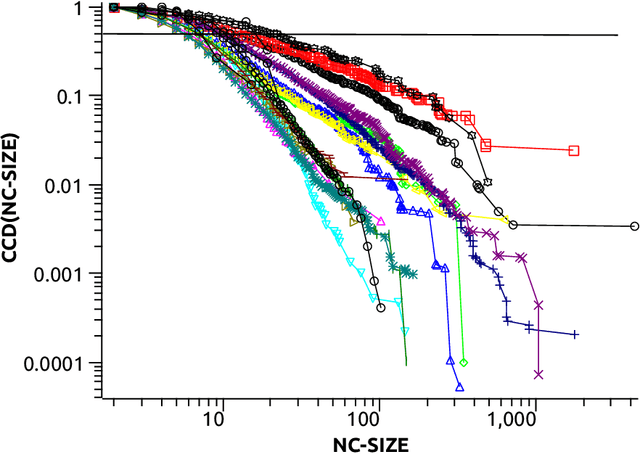
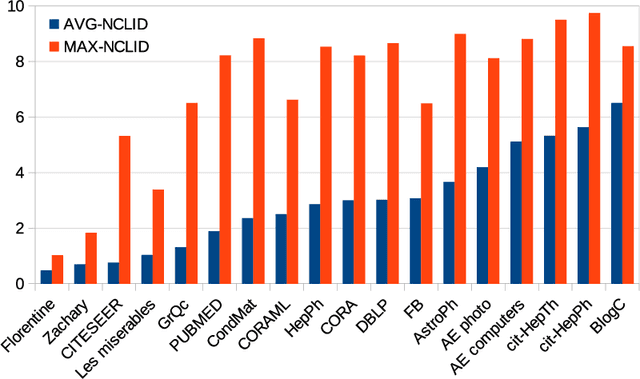
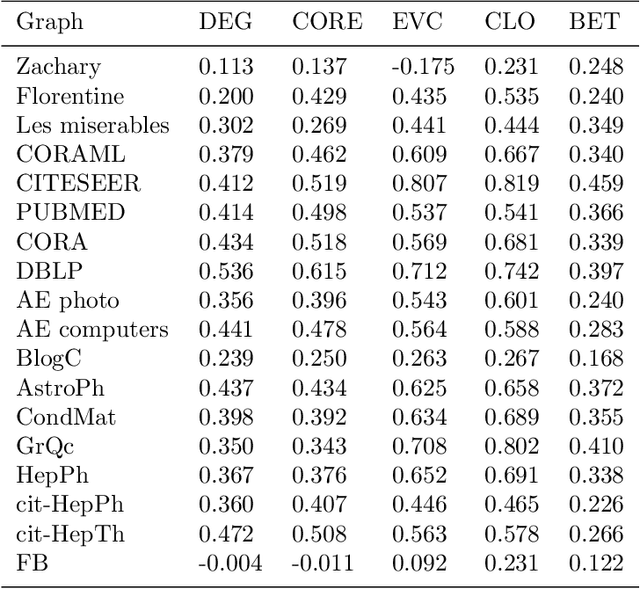
The notion of local intrinsic dimensionality (LID) is an important advancement in data dimensionality analysis, with applications in data mining, machine learning and similarity search problems. Existing distance-based LID estimators were designed for tabular datasets encompassing data points represented as vectors in a Euclidean space. After discussing their limitations for graph-structured data considering graph embeddings and graph distances, we propose NC-LID, a novel LID-related measure for quantifying the discriminatory power of the shortest-path distance with respect to natural communities of nodes as their intrinsic localities. It is shown how this measure can be used to design LID-aware graph embedding algorithms by formulating two LID-elastic variants of node2vec with personalized hyperparameters that are adjusted according to NC-LID values. Our empirical analysis of NC-LID on a large number of real-world graphs shows that this measure is able to point to nodes with high link reconstruction errors in node2vec embeddings better than node centrality metrics. The experimental evaluation also shows that the proposed LID-elastic node2vec extensions improve node2vec by better preserving graph structure in generated embeddings.

The Influence of Global Constraints on Similarity Measures for Time-Series Databases

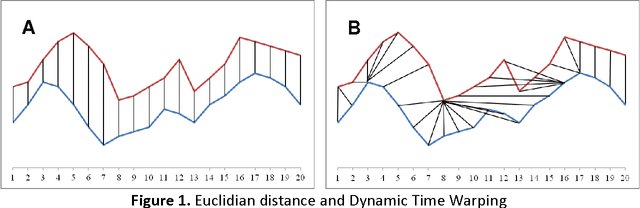
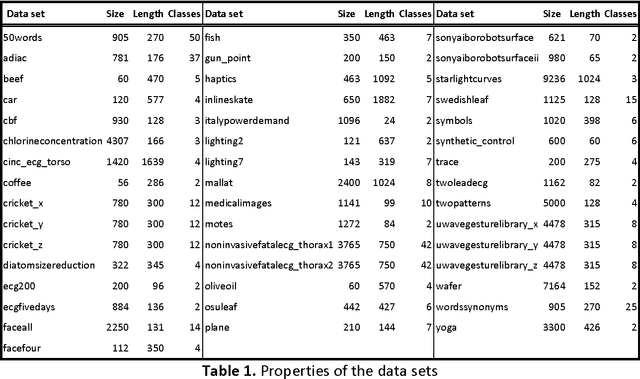
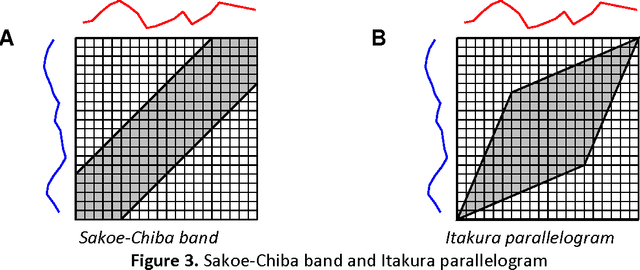
A time series consists of a series of values or events obtained over repeated measurements in time. Analysis of time series represents and important tool in many application areas, such as stock market analysis, process and quality control, observation of natural phenomena, medical treatments, etc. A vital component in many types of time-series analysis is the choice of an appropriate distance/similarity measure. Numerous measures have been proposed to date, with the most successful ones based on dynamic programming. Being of quadratic time complexity, however, global constraints are often employed to limit the search space in the matrix during the dynamic programming procedure, in order to speed up computation. Furthermore, it has been reported that such constrained measures can also achieve better accuracy. In this paper, we investigate two representative time-series distance/similarity measures based on dynamic programming, Dynamic Time Warping (DTW) and Longest Common Subsequence (LCS), and the effects of global constraints on them. Through extensive experiments on a large number of time-series data sets, we demonstrate how global constrains can significantly reduce the computation time of DTW and LCS. We also show that, if the constraint parameter is tight enough (less than 10-15% of time-series length), the constrained measure becomes significantly different from its unconstrained counterpart, in the sense of producing qualitatively different 1-nearest neighbor graphs. This observation explains the potential for accuracy gains when using constrained measures, highlighting the need for careful tuning of constraint parameters in order to achieve a good trade-off between speed and accuracy.