CORTEX: A Cost-Sensitive Rule and Tree Extraction Method

Tree-based and rule-based machine learning models play pivotal roles in explainable artificial intelligence (XAI) due to their unique ability to provide explanations in the form of tree or rule sets that are easily understandable and interpretable, making them essential for applications in which trust in model decisions is necessary. These transparent models are typically used in surrogate modeling, a post-hoc XAI approach for explaining the logic of black-box models, enabling users to comprehend and trust complex predictive systems while maintaining competitive performance. This study proposes the Cost-Sensitive Rule and Tree Extraction (CORTEX) method, a novel rule-based XAI algorithm grounded in the multi-class cost-sensitive decision tree (CSDT) method. The original version of the CSDT is extended to classification problems with more than two classes by inducing the concept of an n-dimensional class-dependent cost matrix. The performance of CORTEX as a rule-extractor XAI method is compared to other post-hoc tree and rule extraction methods across several datasets with different numbers of classes. Several quantitative evaluation metrics are employed to assess the explainability of generated rule sets. Our findings demonstrate that CORTEX is competitive with other tree-based methods and can be superior to other rule-based methods across different datasets. The extracted rule sets suggest the advantages of using the CORTEX method over other methods by producing smaller rule sets with shorter rules on average across datasets with a diverse number of classes. Overall, the results underscore the potential of CORTEX as a powerful XAI tool for scenarios that require the generation of clear, human-understandable rules while maintaining good predictive performance.

Local Intrinsic Dimensionality for Dynamic Graph Embeddings

The notion of local intrinsic dimensionality (LID) has important theoretical implications and practical applications in the fields of data mining and machine learning. Recent research efforts indicate that LID measures defined for graphs can improve graph representational learning methods based on random walks. In this paper, we discuss how NC-LID, a LID measure designed for static graphs, can be adapted for dynamic networks. Focusing on dynnode2vec as the most representative dynamic graph embedding method based on random walks, we examine correlations between NC-LID and the intrinsic quality of 10 real-world dynamic network embeddings. The obtained results show that NC-LID can be used as a good indicator of nodes whose embedding vectors do not tend to preserve temporal graph structure well. Thus, our empirical findings constitute the first step towards LID-aware dynamic graph embedding methods.

Hub-aware Random Walk Graph Embedding Methods for Classification

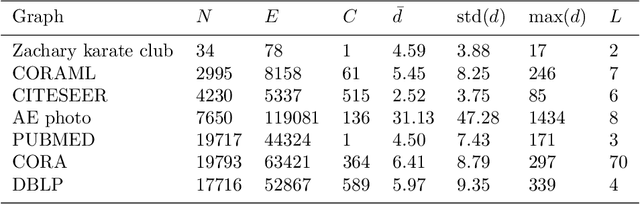
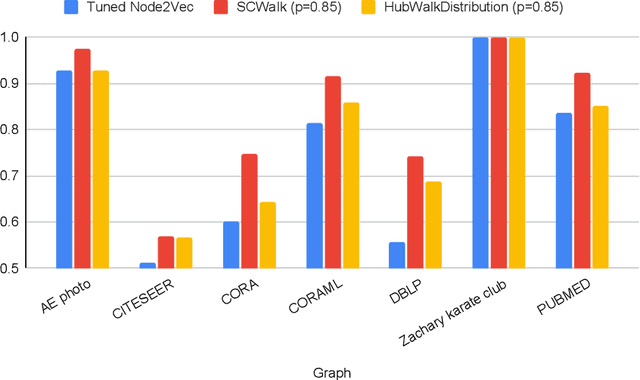
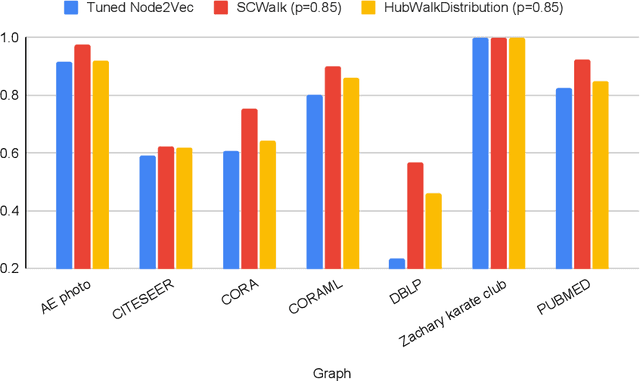
In the last two decades we are witnessing a huge increase of valuable big data structured in the form of graphs or networks. To apply traditional machine learning and data analytic techniques to such data it is necessary to transform graphs into vector-based representations that preserve the most essential structural properties of graphs. For this purpose, a large number of graph embedding methods have been proposed in the literature. Most of them produce general-purpose embeddings suitable for a variety of applications such as node clustering, node classification, graph visualisation and link prediction. In this paper, we propose two novel graph embedding algorithms based on random walks that are specifically designed for the node classification problem. Random walk sampling strategies of the proposed algorithms have been designed to pay special attention to hubs -- high-degree nodes that have the most critical role for the overall connectedness in large-scale graphs. The proposed methods are experimentally evaluated by analyzing the classification performance of three classification algorithms trained on embeddings of real-world networks. The obtained results indicate that our methods considerably improve the predictive power of examined classifiers compared to currently the most popular random walk method for generating general-purpose graph embeddings (node2vec).

Local Intrinsic Dimensionality Measures for Graphs, with Applications to Graph Embeddings

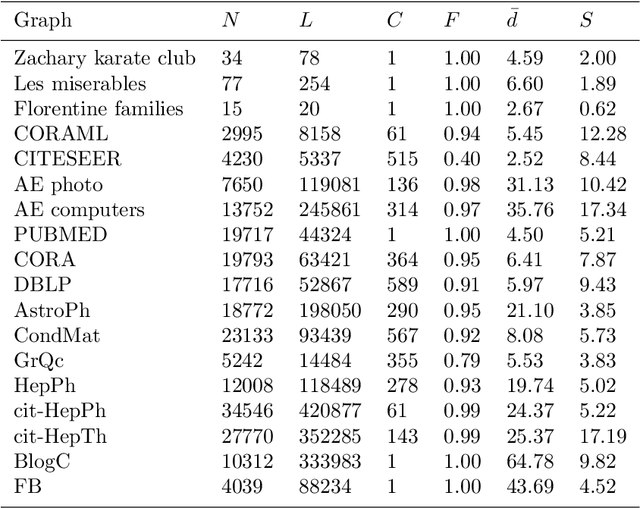
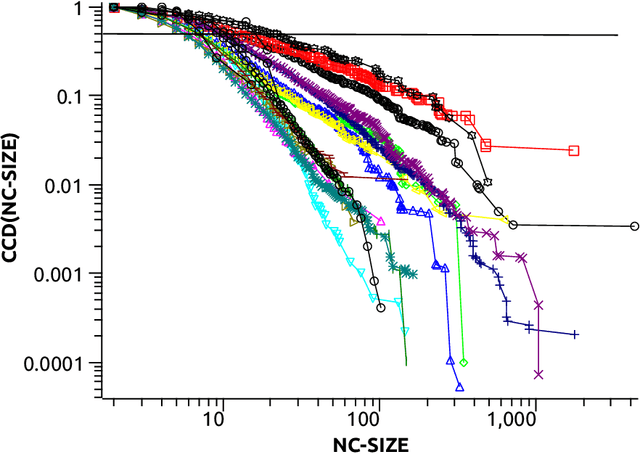
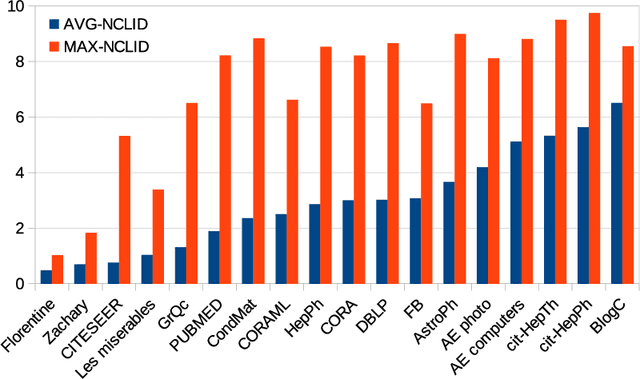
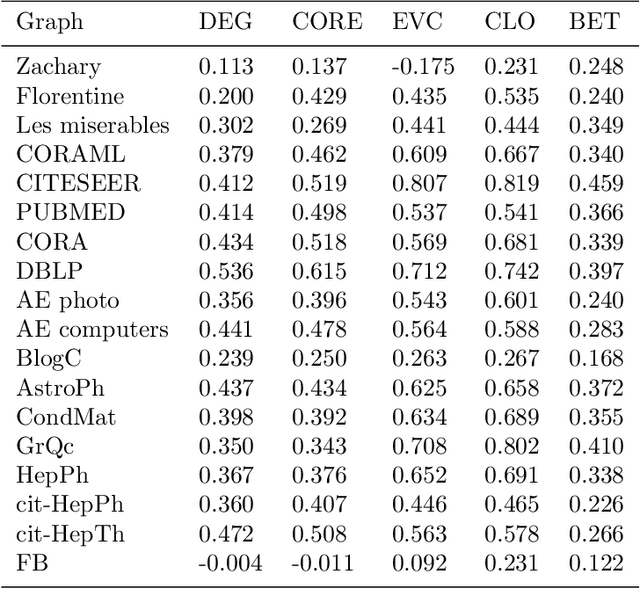
The notion of local intrinsic dimensionality (LID) is an important advancement in data dimensionality analysis, with applications in data mining, machine learning and similarity search problems. Existing distance-based LID estimators were designed for tabular datasets encompassing data points represented as vectors in a Euclidean space. After discussing their limitations for graph-structured data considering graph embeddings and graph distances, we propose NC-LID, a novel LID-related measure for quantifying the discriminatory power of the shortest-path distance with respect to natural communities of nodes as their intrinsic localities. It is shown how this measure can be used to design LID-aware graph embedding algorithms by formulating two LID-elastic variants of node2vec with personalized hyperparameters that are adjusted according to NC-LID values. Our empirical analysis of NC-LID on a large number of real-world graphs shows that this measure is able to point to nodes with high link reconstruction errors in node2vec embeddings better than node centrality metrics. The experimental evaluation also shows that the proposed LID-elastic node2vec extensions improve node2vec by better preserving graph structure in generated embeddings.

Tax Evasion Risk Management Using a Hybrid Unsupervised Outlier Detection Method

Big data methods are becoming an important tool for tax fraud detection around the world. Unsupervised learning approach is the dominant framework due to the lack of label and ground truth in corresponding data sets although these methods suffer from low interpretability. HUNOD, a novel hybrid unsupervised outlier detection method for tax evasion risk management, is presented in this paper. In contrast to previous methods proposed in the literature, the HUNOD method combines two outlier detection approaches based on two different machine learning designs (i.e, clustering and representational learning) to detect and internally validate outliers in a given tax dataset. The HUNOD method allows its users to incorporate relevant domain knowledge into both constituent outlier detection approaches in order to detect outliers relevant for a given economic context. The interpretability of obtained outliers is achieved by training explainable-by-design surrogate models over results of unsupervised outlier detection methods. The experimental evaluation of the HUNOD method is conducted on two datasets derived from the database on individual personal income tax declarations collected by the Tax Administration of Serbia. The obtained results show that the method indicates between 90% and 98% internally validated outliers depending on the clustering configuration and employed regularization mechanisms for representational learning.