Vladimir Kurbalija
Local Intrinsic Dimensionality Measures for Graphs, with Applications to Graph Embeddings
Aug 25, 2022
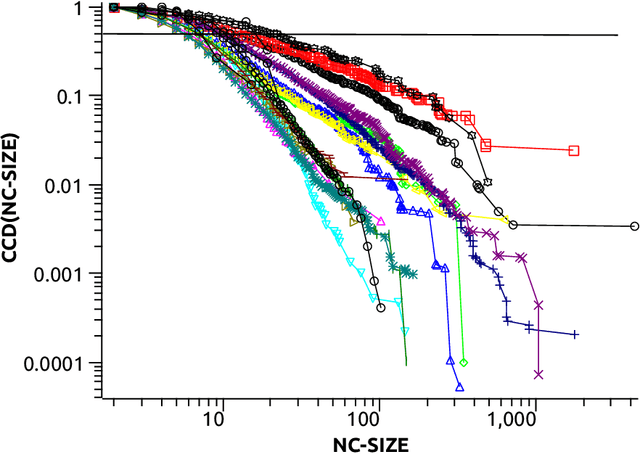
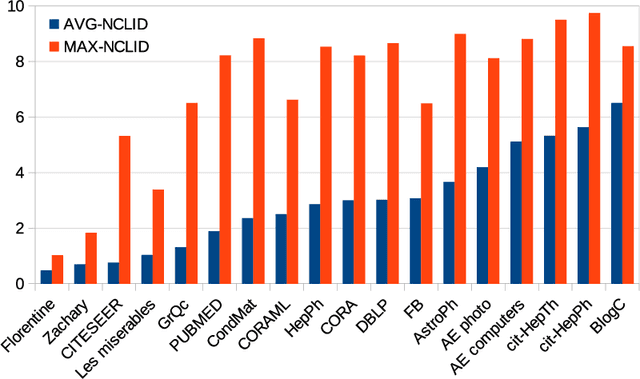
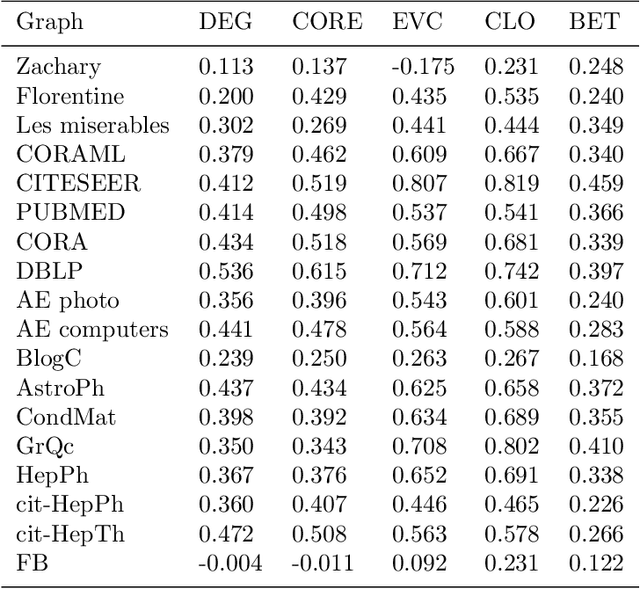
Abstract:The notion of local intrinsic dimensionality (LID) is an important advancement in data dimensionality analysis, with applications in data mining, machine learning and similarity search problems. Existing distance-based LID estimators were designed for tabular datasets encompassing data points represented as vectors in a Euclidean space. After discussing their limitations for graph-structured data considering graph embeddings and graph distances, we propose NC-LID, a novel LID-related measure for quantifying the discriminatory power of the shortest-path distance with respect to natural communities of nodes as their intrinsic localities. It is shown how this measure can be used to design LID-aware graph embedding algorithms by formulating two LID-elastic variants of node2vec with personalized hyperparameters that are adjusted according to NC-LID values. Our empirical analysis of NC-LID on a large number of real-world graphs shows that this measure is able to point to nodes with high link reconstruction errors in node2vec embeddings better than node centrality metrics. The experimental evaluation also shows that the proposed LID-elastic node2vec extensions improve node2vec by better preserving graph structure in generated embeddings.
The Influence of Global Constraints on Similarity Measures for Time-Series Databases
Dec 25, 2013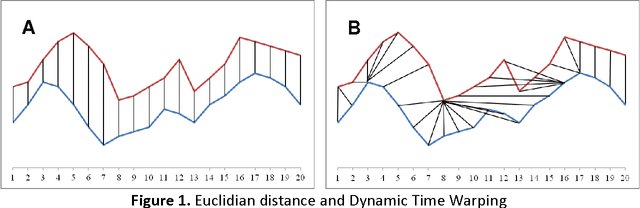
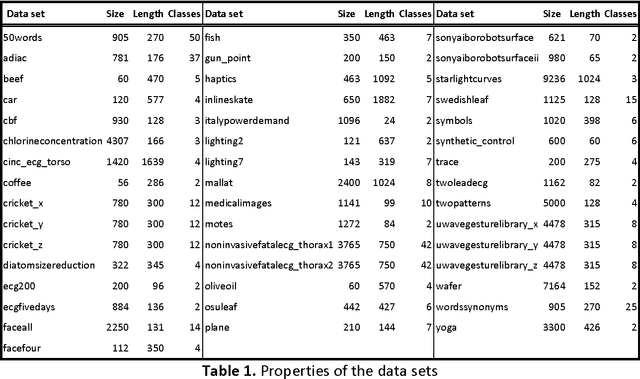

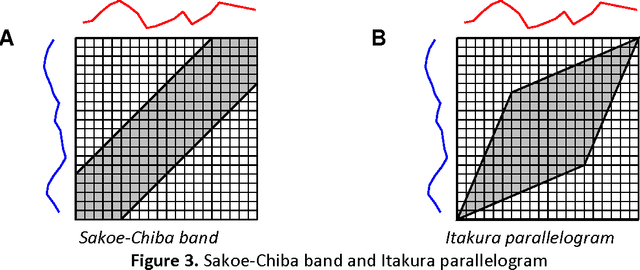
Abstract:A time series consists of a series of values or events obtained over repeated measurements in time. Analysis of time series represents and important tool in many application areas, such as stock market analysis, process and quality control, observation of natural phenomena, medical treatments, etc. A vital component in many types of time-series analysis is the choice of an appropriate distance/similarity measure. Numerous measures have been proposed to date, with the most successful ones based on dynamic programming. Being of quadratic time complexity, however, global constraints are often employed to limit the search space in the matrix during the dynamic programming procedure, in order to speed up computation. Furthermore, it has been reported that such constrained measures can also achieve better accuracy. In this paper, we investigate two representative time-series distance/similarity measures based on dynamic programming, Dynamic Time Warping (DTW) and Longest Common Subsequence (LCS), and the effects of global constraints on them. Through extensive experiments on a large number of time-series data sets, we demonstrate how global constrains can significantly reduce the computation time of DTW and LCS. We also show that, if the constraint parameter is tight enough (less than 10-15% of time-series length), the constrained measure becomes significantly different from its unconstrained counterpart, in the sense of producing qualitatively different 1-nearest neighbor graphs. This observation explains the potential for accuracy gains when using constrained measures, highlighting the need for careful tuning of constraint parameters in order to achieve a good trade-off between speed and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge