Local Intrinsic Dimensionality Measures for Graphs, with Applications to Graph Embeddings
Paper and Code
Aug 25, 2022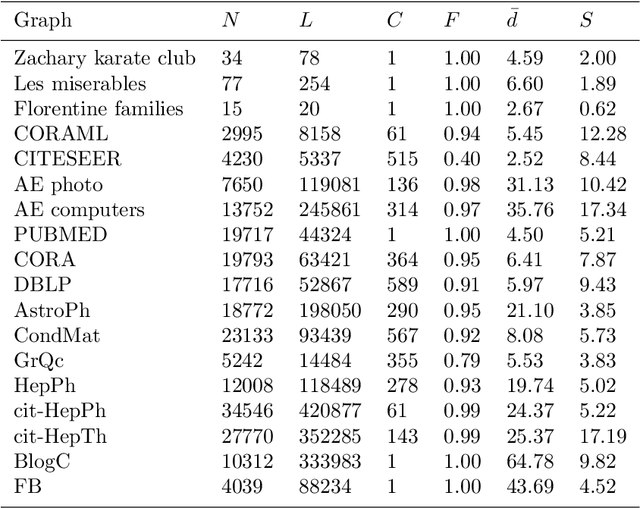
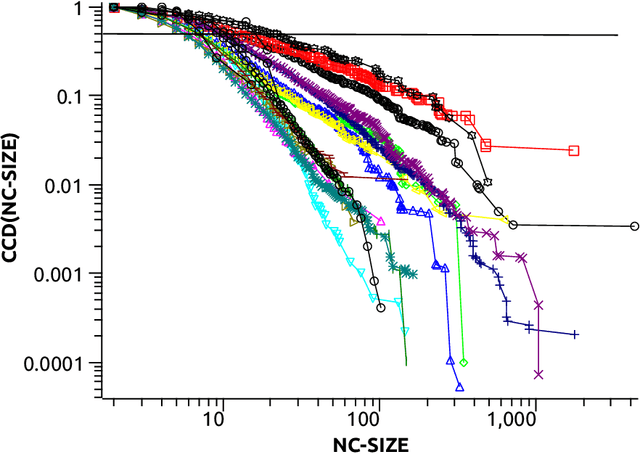
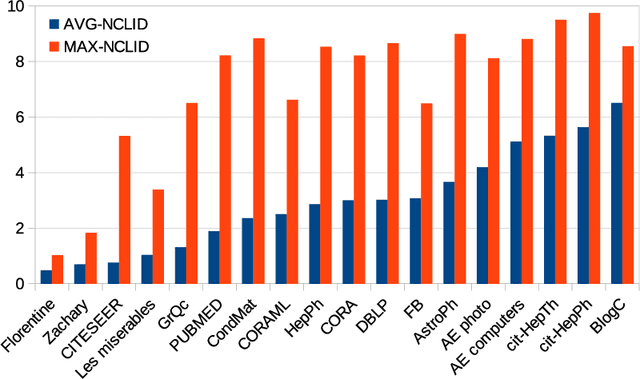
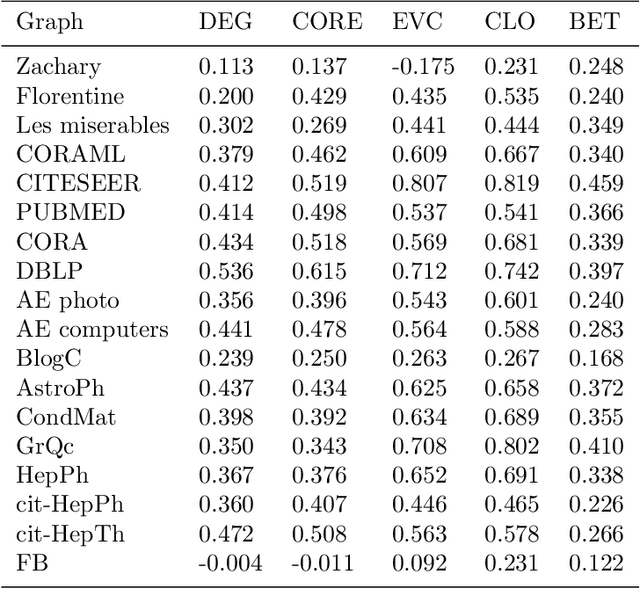
The notion of local intrinsic dimensionality (LID) is an important advancement in data dimensionality analysis, with applications in data mining, machine learning and similarity search problems. Existing distance-based LID estimators were designed for tabular datasets encompassing data points represented as vectors in a Euclidean space. After discussing their limitations for graph-structured data considering graph embeddings and graph distances, we propose NC-LID, a novel LID-related measure for quantifying the discriminatory power of the shortest-path distance with respect to natural communities of nodes as their intrinsic localities. It is shown how this measure can be used to design LID-aware graph embedding algorithms by formulating two LID-elastic variants of node2vec with personalized hyperparameters that are adjusted according to NC-LID values. Our empirical analysis of NC-LID on a large number of real-world graphs shows that this measure is able to point to nodes with high link reconstruction errors in node2vec embeddings better than node centrality metrics. The experimental evaluation also shows that the proposed LID-elastic node2vec extensions improve node2vec by better preserving graph structure in generated embeddings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge