New classes of the greedy-applicable arm feature distributions in the sparse linear bandit problem

We consider the sparse contextual bandit problem where arm feature affects reward through the inner product of sparse parameters. Recent studies have developed sparsity-agnostic algorithms based on the greedy arm selection policy. However, the analysis of these algorithms requires strong assumptions on the arm feature distribution to ensure that the greedily selected samples are sufficiently diverse; One of the most common assumptions, relaxed symmetry, imposes approximate origin-symmetry on the distribution, which cannot allow distributions that has origin-asymmetric support. In this paper, we show that the greedy algorithm is applicable to a wider range of the arm feature distributions from two aspects. Firstly, we show that a mixture distribution that has a greedy-applicable component is also greedy-applicable. Second, we propose new distribution classes, related to Gaussian mixture, discrete, and radial distribution, for which the sample diversity is guaranteed. The proposed classes can describe distributions with origin-asymmetric support and, in conjunction with the first claim, provide theoretical guarantees of the greedy policy for a very wide range of the arm feature distributions.

A Neighbourhood-Aware Differential Privacy Mechanism for Static Word Embeddings

We propose a Neighbourhood-Aware Differential Privacy (NADP) mechanism considering the neighbourhood of a word in a pretrained static word embedding space to determine the minimal amount of noise required to guarantee a specified privacy level. We first construct a nearest neighbour graph over the words using their embeddings, and factorise it into a set of connected components (i.e. neighbourhoods). We then separately apply different levels of Gaussian noise to the words in each neighbourhood, determined by the set of words in that neighbourhood. Experiments show that our proposed NADP mechanism consistently outperforms multiple previously proposed DP mechanisms such as Laplacian, Gaussian, and Mahalanobis in multiple downstream tasks, while guaranteeing higher levels of privacy.

Intrinsic Dimensionality Estimation within Tight Localities: A Theoretical and Experimental Analysis

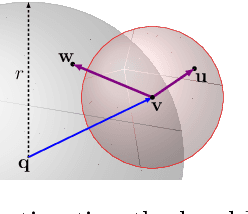
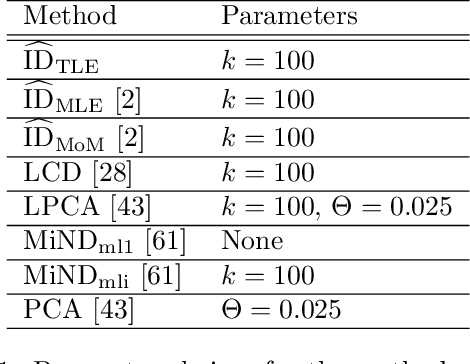
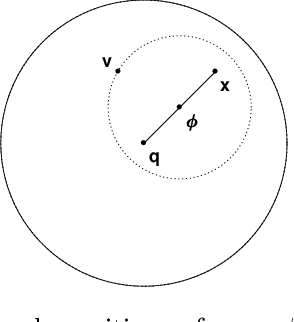
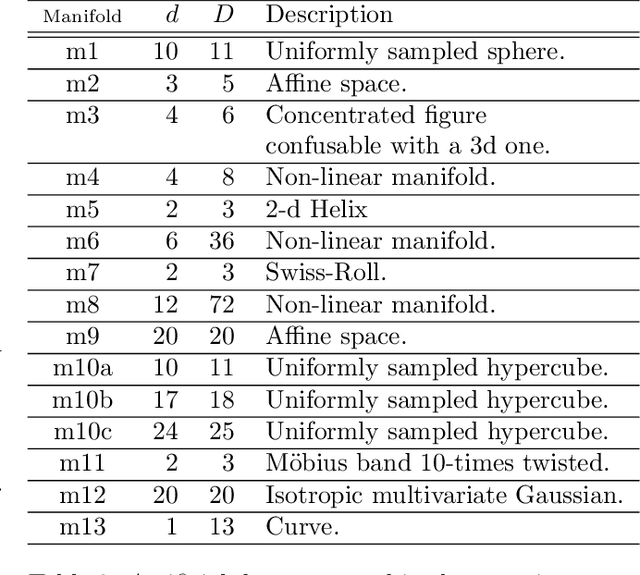
Accurate estimation of Intrinsic Dimensionality (ID) is of crucial importance in many data mining and machine learning tasks, including dimensionality reduction, outlier detection, similarity search and subspace clustering. However, since their convergence generally requires sample sizes (that is, neighborhood sizes) on the order of hundreds of points, existing ID estimation methods may have only limited usefulness for applications in which the data consists of many natural groups of small size. In this paper, we propose a local ID estimation strategy stable even for `tight' localities consisting of as few as 20 sample points. The estimator applies MLE techniques over all available pairwise distances among the members of the sample, based on a recent extreme-value-theoretic model of intrinsic dimensionality, the Local Intrinsic Dimension (LID). Our experimental results show that our proposed estimation technique can achieve notably smaller variance, while maintaining comparable levels of bias, at much smaller sample sizes than state-of-the-art estimators.

Online Task Assignment Problems with Reusable Resources

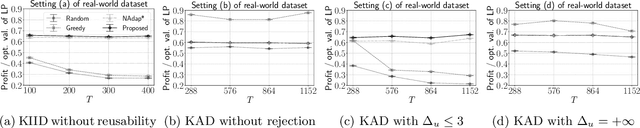
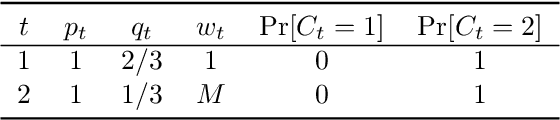
We study online task assignment problem with reusable resources, motivated by practical applications such as ridesharing, crowdsourcing and job hiring. In the problem, we are given a set of offline vertices (agents), and, at each time, an online vertex (task) arrives randomly according to a known time-dependent distribution. Upon arrival, we assign the task to agents immediately and irrevocably. The goal of the problem is to maximize the expected total profit produced by completed tasks. The key features of our problem are (1) an agent is reusable, i.e., an agent comes back to the market after completing the assigned task, (2) an agent may reject the assigned task to stay the market, and (3) a task may accommodate multiple agents. The setting generalizes that of existing work in which an online task is assigned to one agent under (1). In this paper, we propose an online algorithm that is $1/2$-competitive for the above setting, which is tight. Moreover, when each agent can reject assigned tasks at most $\Delta$ times, the algorithm is shown to have the competitive ratio $\Delta/(3\Delta-1)\geq 1/3$. We also evaluate our proposed algorithm with numerical experiments.

RelWalk A Latent Variable Model Approach to Knowledge Graph Embedding

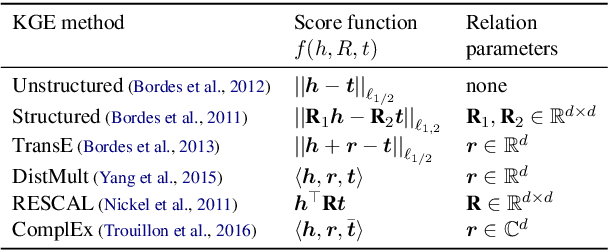
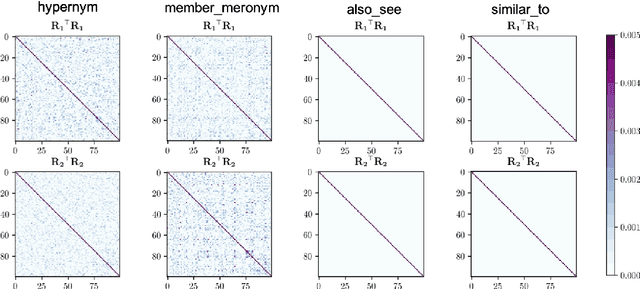
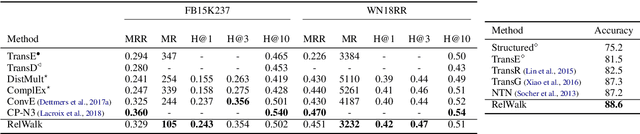
Embedding entities and relations of a knowledge graph in a low-dimensional space has shown impressive performance in predicting missing links between entities. Although progresses have been achieved, existing methods are heuristically motivated and theoretical understanding of such embeddings is comparatively underdeveloped. This paper extends the random walk model (Arora et al., 2016a) of word embeddings to Knowledge Graph Embeddings (KGEs) to derive a scoring function that evaluates the strength of a relation R between two entities h (head) and t (tail). Moreover, we show that marginal loss minimisation, a popular objective used in much prior work in KGE, follows naturally from the log-likelihood ratio maximisation under the probabilities estimated from the KGEs according to our theoretical relationship. We propose a learning objective motivated by the theoretical analysis to learn KGEs from a given knowledge graph. Using the derived objective, accurate KGEs are learnt from FB15K237 and WN18RR benchmark datasets, providing empirical evidence in support of the theory.

Near-Optimal Regret Bounds for Contextual Combinatorial Semi-Bandits with Linear Payoff Functions

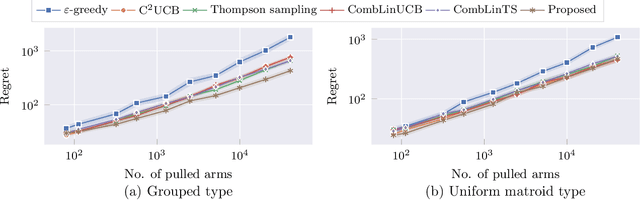
The contextual combinatorial semi-bandit problem with linear payoff functions is a decision-making problem in which a learner chooses a set of arms with the feature vectors in each round under given constraints so as to maximize the sum of rewards of arms. Several existing algorithms have regret bounds that are optimal with respect to the number of rounds $T$. However, there is a gap of $\tilde{O}(\max(\sqrt{d}, \sqrt{k}))$ between the current best upper and lower bounds, where $d$ is the dimension of the feature vectors, $k$ is the number of the chosen arms in a round, and $\tilde{O}(\cdot)$ ignores the logarithmic factors. The dependence of $k$ and $d$ is of practical importance because $k$ may be larger than $T$ in real-world applications such as recommender systems. In this paper, we fill the gap by improving the upper and lower bounds. More precisely, we show that the C${}^2$UCB algorithm proposed by Qin, Chen, and Zhu (2014) has the optimal regret bound $\tilde{O}(d\sqrt{kT} + dk)$ for the partition matroid constraints. For general constraints, we propose an algorithm that modifies the reward estimates of arms in the C${}^2$UCB algorithm and demonstrate that it enjoys the optimal regret bound for a more general problem that can take into account other objectives simultaneously. We also show that our technique would be applicable to related problems. Numerical experiments support our theoretical results and considerations.

How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks

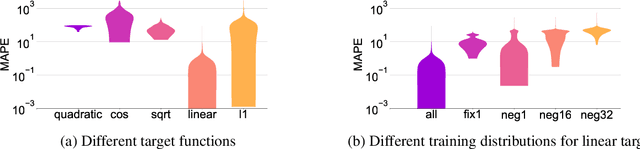
We study how neural networks trained by gradient descent extrapolate, i.e., what they learn outside the support of the training distribution. Previous works report mixed empirical results when extrapolating with neural networks: while multilayer perceptrons (MLPs) do not extrapolate well in certain simple tasks, Graph Neural Network (GNN), a structured network with MLP modules, has shown some success in more complex tasks. Working towards a theoretical explanation, we identify conditions under which MLPs and GNNs extrapolate well. First, we quantify the observation that ReLU MLPs quickly converge to linear functions along any direction from the origin, which implies that ReLU MLPs do not extrapolate most non-linear functions. But, they can provably learn a linear target function when the training distribution is sufficiently "diverse". Second, in connection to analyzing successes and limitations of GNNs, these results suggest a hypothesis for which we provide theoretical and empirical evidence: the success of GNNs in extrapolating algorithmic tasks to new data (e.g., larger graphs or edge weights) relies on encoding task-specific non-linearities in the architecture or features.

Anonymising Queries by Semantic Decomposition

Protecting the privacy of search engine users is an important requirement in many information retrieval scenarios. A user might not want a search engine to guess his or her information need despite requesting relevant results. We propose a method to protect the privacy of search engine users by decomposing the queries using semantically \emph{related} and unrelated \emph{distractor} terms. Instead of a single query, the search engine receives multiple decomposed query terms. Next, we reconstruct the search results relevant to the original query term by aggregating the search results retrieved for the decomposed query terms. We show that the word embeddings learnt using a distributed representation learning method can be used to find semantically related and distractor query terms. We derive the relationship between the \emph{anonymity} achieved through the proposed query anonymisation method and the \emph{reconstructability} of the original search results using the decomposed queries. We analytically study the risk of discovering the search engine users' information intents under the proposed query anonymisation method, and empirically evaluate its robustness against clustering-based attacks. Our experimental results show that the proposed method can accurately reconstruct the search results for user queries, without compromising the privacy of the search engine users.

Are Girls Neko or Shōjo? Cross-Lingual Alignment of Non-Isomorphic Embeddings with Iterative Normalization

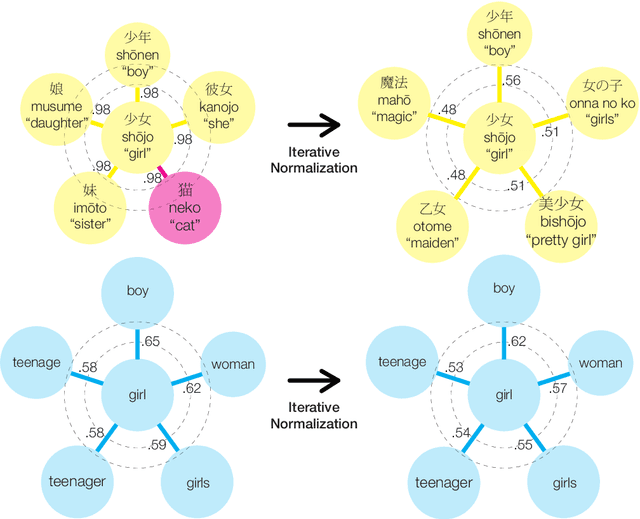
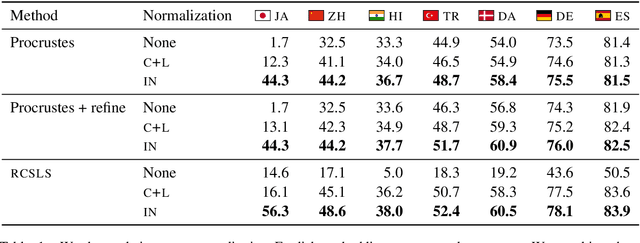
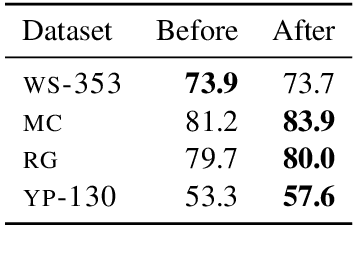
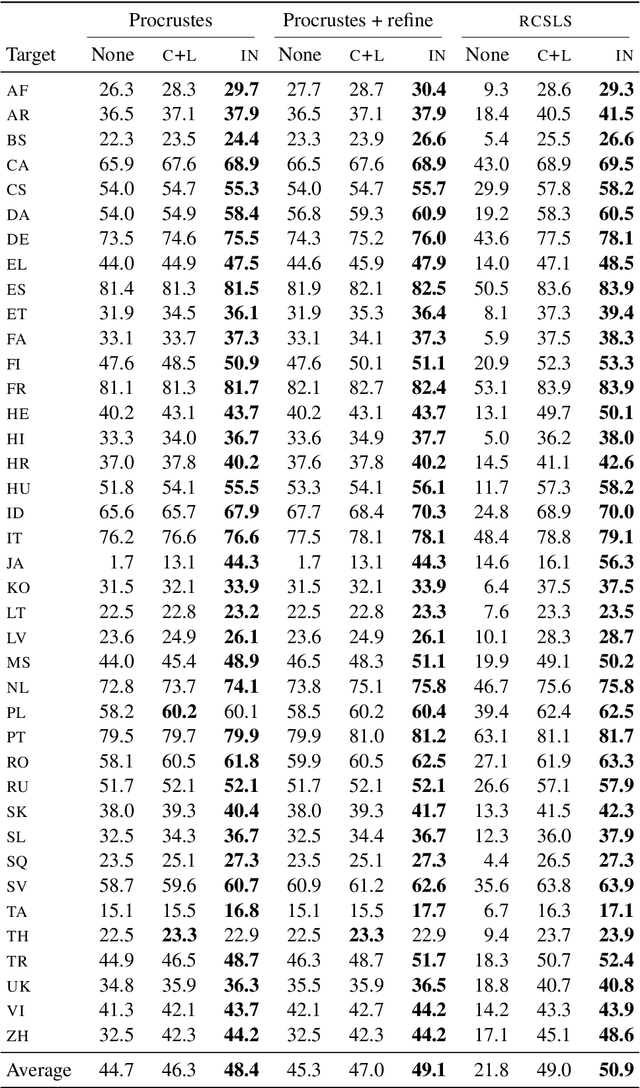
Cross-lingual word embeddings (CLWE) underlie many multilingual natural language processing systems, often through orthogonal transformations of pre-trained monolingual embeddings. However, orthogonal mapping only works on language pairs whose embeddings are naturally isomorphic. For non-isomorphic pairs, our method (Iterative Normalization) transforms monolingual embeddings to make orthogonal alignment easier by simultaneously enforcing that (1) individual word vectors are unit length, and (2) each language's average vector is zero. Iterative Normalization consistently improves word translation accuracy of three CLWE methods, with the largest improvement observed on English-Japanese (from 2% to 44% test accuracy).

What Can Neural Networks Reason About?

Neural networks have successfully been applied to solving reasoning tasks, ranging from learning simple concepts like "close to", to intricate questions whose reasoning procedures resemble algorithms. Empirically, not all network structures work equally well for reasoning. For example, Graph Neural Networks have achieved impressive empirical results, while less structured neural networks may fail to learn to reason. Theoretically, there is currently limited understanding of the interplay between reasoning tasks and network learning. In this paper, we develop a framework to characterize which tasks a neural network can learn well, by studying how well its structure aligns with the algorithmic structure of the relevant reasoning procedure. This suggests that Graph Neural Networks can learn dynamic programming, a powerful algorithmic strategy that solves a broad class of reasoning problems, such as relational question answering, sorting, intuitive physics, and shortest paths. Our perspective also implies strategies to design neural architectures for complex reasoning. On several abstract reasoning tasks, we see empirically that our theory aligns well with practice.