Best-of-Three-Worlds Linear Bandit Algorithm with Variance-Adaptive Regret Bounds

This paper proposes a linear bandit algorithm that is adaptive to environments at two different levels of hierarchy. At the higher level, the proposed algorithm adapts to a variety of types of environments. More precisely, it achieves best-of-three-worlds regret bounds, i.e., of ${O}(\sqrt{T \log T})$ for adversarial environments and of $O(\frac{\log T}{\Delta_{\min}} + \sqrt{\frac{C \log T}{\Delta_{\min}}})$ for stochastic environments with adversarial corruptions, where $T$, $\Delta_{\min}$, and $C$ denote, respectively, the time horizon, the minimum sub-optimality gap, and the total amount of the corruption. Note that polynomial factors in the dimensionality are omitted here. At the lower level, in each of the adversarial and stochastic regimes, the proposed algorithm adapts to certain environmental characteristics, thereby performing better. The proposed algorithm has data-dependent regret bounds that depend on all of the cumulative loss for the optimal action, the total quadratic variation, and the path-length of the loss vector sequence. In addition, for stochastic environments, the proposed algorithm has a variance-adaptive regret bound of $O(\frac{\sigma^2 \log T}{\Delta_{\min}})$ as well, where $\sigma^2$ denotes the maximum variance of the feedback loss. The proposed algorithm is based on the SCRiBLe algorithm. By incorporating into this a new technique we call scaled-up sampling, we obtain high-level adaptability, and by incorporating the technique of optimistic online learning, we obtain low-level adaptability.

Online Task Assignment Problems with Reusable Resources

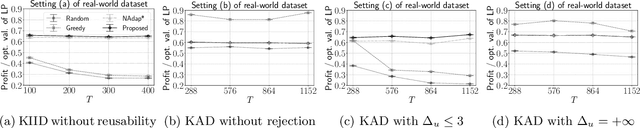
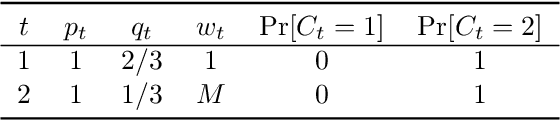
We study online task assignment problem with reusable resources, motivated by practical applications such as ridesharing, crowdsourcing and job hiring. In the problem, we are given a set of offline vertices (agents), and, at each time, an online vertex (task) arrives randomly according to a known time-dependent distribution. Upon arrival, we assign the task to agents immediately and irrevocably. The goal of the problem is to maximize the expected total profit produced by completed tasks. The key features of our problem are (1) an agent is reusable, i.e., an agent comes back to the market after completing the assigned task, (2) an agent may reject the assigned task to stay the market, and (3) a task may accommodate multiple agents. The setting generalizes that of existing work in which an online task is assigned to one agent under (1). In this paper, we propose an online algorithm that is $1/2$-competitive for the above setting, which is tight. Moreover, when each agent can reject assigned tasks at most $\Delta$ times, the algorithm is shown to have the competitive ratio $\Delta/(3\Delta-1)\geq 1/3$. We also evaluate our proposed algorithm with numerical experiments.

Near-Optimal Regret Bounds for Contextual Combinatorial Semi-Bandits with Linear Payoff Functions

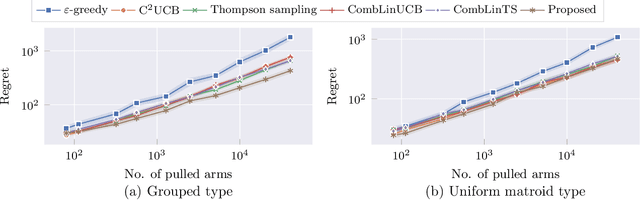
The contextual combinatorial semi-bandit problem with linear payoff functions is a decision-making problem in which a learner chooses a set of arms with the feature vectors in each round under given constraints so as to maximize the sum of rewards of arms. Several existing algorithms have regret bounds that are optimal with respect to the number of rounds $T$. However, there is a gap of $\tilde{O}(\max(\sqrt{d}, \sqrt{k}))$ between the current best upper and lower bounds, where $d$ is the dimension of the feature vectors, $k$ is the number of the chosen arms in a round, and $\tilde{O}(\cdot)$ ignores the logarithmic factors. The dependence of $k$ and $d$ is of practical importance because $k$ may be larger than $T$ in real-world applications such as recommender systems. In this paper, we fill the gap by improving the upper and lower bounds. More precisely, we show that the C${}^2$UCB algorithm proposed by Qin, Chen, and Zhu (2014) has the optimal regret bound $\tilde{O}(d\sqrt{kT} + dk)$ for the partition matroid constraints. For general constraints, we propose an algorithm that modifies the reward estimates of arms in the C${}^2$UCB algorithm and demonstrate that it enjoys the optimal regret bound for a more general problem that can take into account other objectives simultaneously. We also show that our technique would be applicable to related problems. Numerical experiments support our theoretical results and considerations.

An Arm-Wise Randomization Approach to Combinatorial Linear Semi-Bandits

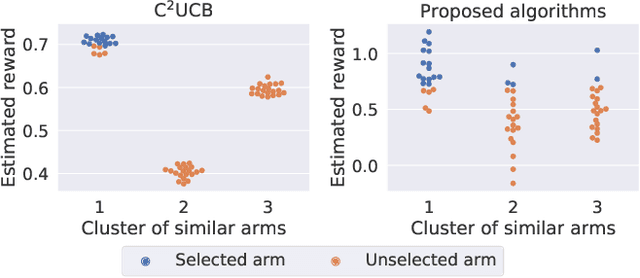
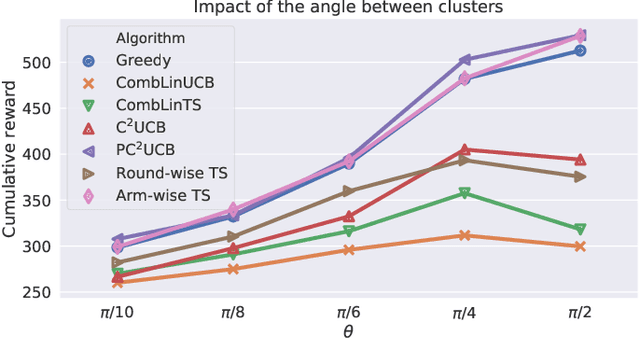
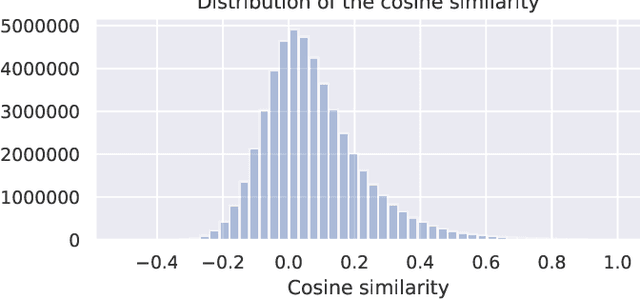
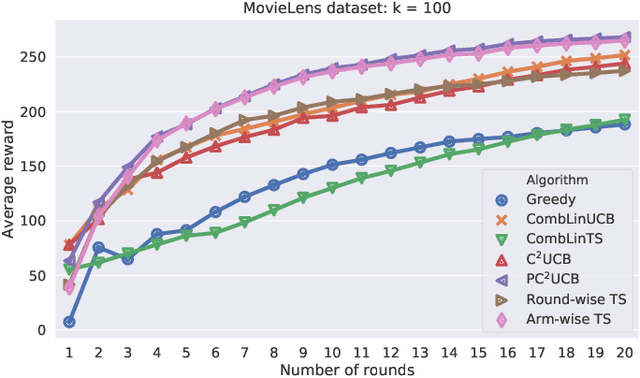
Combinatorial linear semi-bandits (CLS) are widely applicable frameworks of sequential decision-making, in which a learner chooses a subset of arms from a given set of arms associated with feature vectors. Existing algorithms work poorly for the clustered case, in which the feature vectors form several large clusters. This shortcoming is critical in practice because it can be found in many applications, including recommender systems. In this paper, we clarify why such a shortcoming occurs, and we introduce a key technique of arm-wise randomization to overcome it. We propose two algorithms with this technique: the perturbed C${}^2$UCB (PC${}^2$UCB) and the Thompson sampling (TS). Our empirical evaluation with artificial and real-world datasets demonstrates that the proposed algorithms with the arm-wise randomization technique outperform the existing algorithms without this technique, especially for the clustered case. Our contributions also include theoretical analyses that provide high probability asymptotic regret bounds for our algorithms.