An Arm-Wise Randomization Approach to Combinatorial Linear Semi-Bandits
Paper and Code
Sep 10, 2019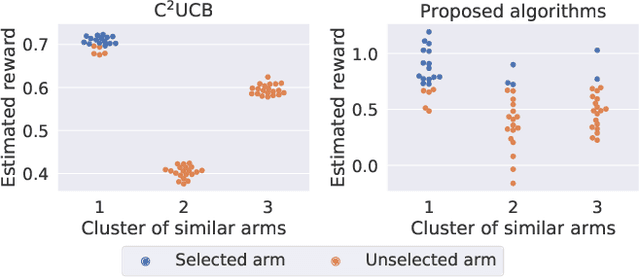
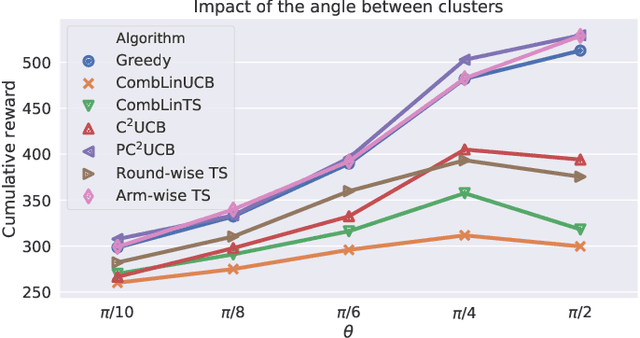
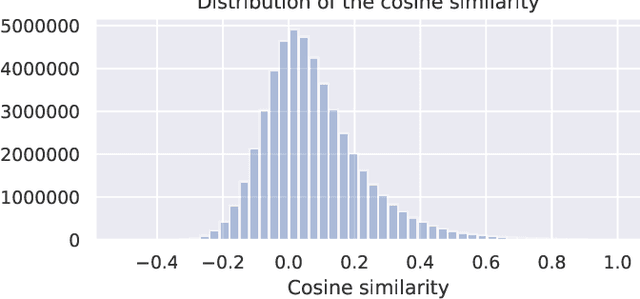
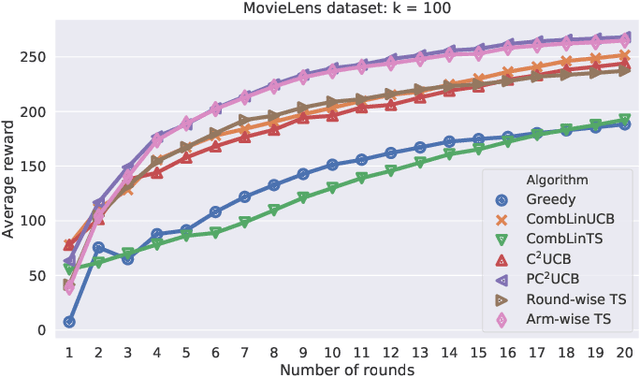
Combinatorial linear semi-bandits (CLS) are widely applicable frameworks of sequential decision-making, in which a learner chooses a subset of arms from a given set of arms associated with feature vectors. Existing algorithms work poorly for the clustered case, in which the feature vectors form several large clusters. This shortcoming is critical in practice because it can be found in many applications, including recommender systems. In this paper, we clarify why such a shortcoming occurs, and we introduce a key technique of arm-wise randomization to overcome it. We propose two algorithms with this technique: the perturbed C${}^2$UCB (PC${}^2$UCB) and the Thompson sampling (TS). Our empirical evaluation with artificial and real-world datasets demonstrates that the proposed algorithms with the arm-wise randomization technique outperform the existing algorithms without this technique, especially for the clustered case. Our contributions also include theoretical analyses that provide high probability asymptotic regret bounds for our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge