New classes of the greedy-applicable arm feature distributions in the sparse linear bandit problem

We consider the sparse contextual bandit problem where arm feature affects reward through the inner product of sparse parameters. Recent studies have developed sparsity-agnostic algorithms based on the greedy arm selection policy. However, the analysis of these algorithms requires strong assumptions on the arm feature distribution to ensure that the greedily selected samples are sufficiently diverse; One of the most common assumptions, relaxed symmetry, imposes approximate origin-symmetry on the distribution, which cannot allow distributions that has origin-asymmetric support. In this paper, we show that the greedy algorithm is applicable to a wider range of the arm feature distributions from two aspects. Firstly, we show that a mixture distribution that has a greedy-applicable component is also greedy-applicable. Second, we propose new distribution classes, related to Gaussian mixture, discrete, and radial distribution, for which the sample diversity is guaranteed. The proposed classes can describe distributions with origin-asymmetric support and, in conjunction with the first claim, provide theoretical guarantees of the greedy policy for a very wide range of the arm feature distributions.

Reforming an Envy-Free Matching

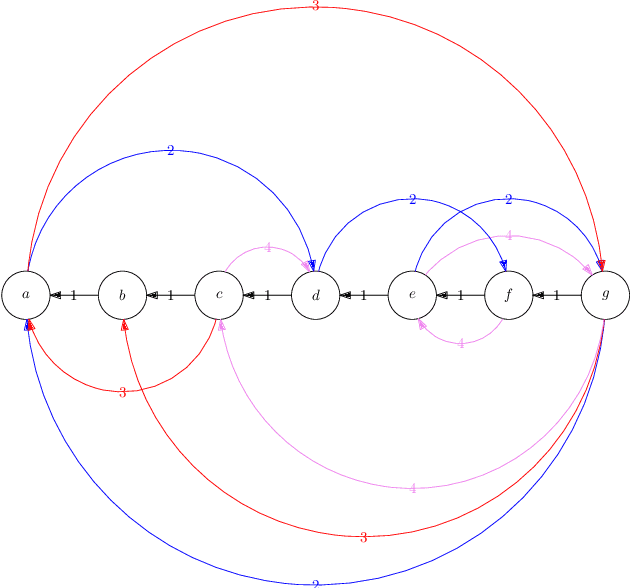
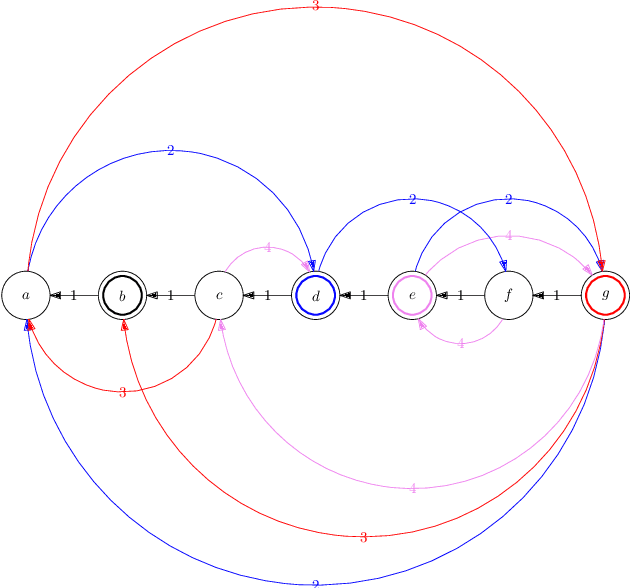
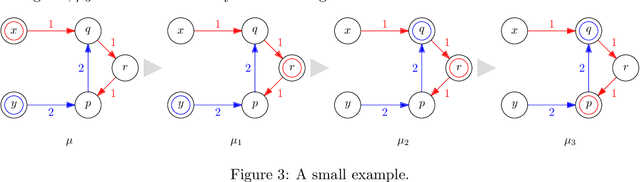
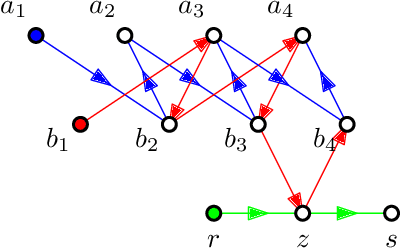
We consider the problem of reforming an envy-free matching when each agent is assigned a single item. Given an envy-free matching, we consider an operation to exchange the item of an agent with an unassigned item preferred by the agent that results in another envy-free matching. We repeat this operation as long as we can. We prove that the resulting envy-free matching is uniquely determined up to the choice of an initial envy-free matching, and can be found in polynomial time. We call the resulting matching a reformist envy-free matching, and then we study a shortest sequence to obtain the reformist envy-free matching from an initial envy-free matching. We prove that a shortest sequence is computationally hard to obtain even when each agent accepts at most four items and each item is accepted by at most three agents. On the other hand, we give polynomial-time algorithms when each agent accepts at most three items or each item is accepted by at most two agents. Inapproximability and fixed-parameter (in)tractability are also discussed.

Online Task Assignment Problems with Reusable Resources

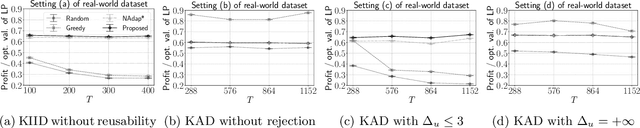
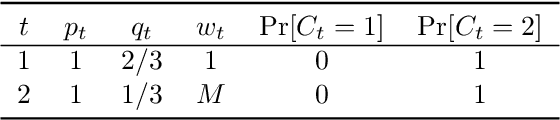
We study online task assignment problem with reusable resources, motivated by practical applications such as ridesharing, crowdsourcing and job hiring. In the problem, we are given a set of offline vertices (agents), and, at each time, an online vertex (task) arrives randomly according to a known time-dependent distribution. Upon arrival, we assign the task to agents immediately and irrevocably. The goal of the problem is to maximize the expected total profit produced by completed tasks. The key features of our problem are (1) an agent is reusable, i.e., an agent comes back to the market after completing the assigned task, (2) an agent may reject the assigned task to stay the market, and (3) a task may accommodate multiple agents. The setting generalizes that of existing work in which an online task is assigned to one agent under (1). In this paper, we propose an online algorithm that is $1/2$-competitive for the above setting, which is tight. Moreover, when each agent can reject assigned tasks at most $\Delta$ times, the algorithm is shown to have the competitive ratio $\Delta/(3\Delta-1)\geq 1/3$. We also evaluate our proposed algorithm with numerical experiments.

Near-Optimal Regret Bounds for Contextual Combinatorial Semi-Bandits with Linear Payoff Functions

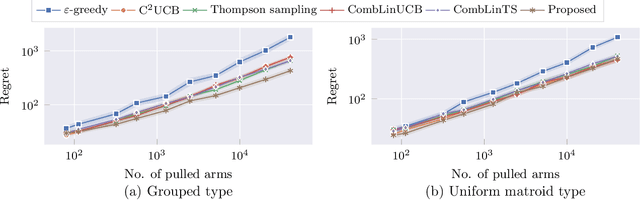
The contextual combinatorial semi-bandit problem with linear payoff functions is a decision-making problem in which a learner chooses a set of arms with the feature vectors in each round under given constraints so as to maximize the sum of rewards of arms. Several existing algorithms have regret bounds that are optimal with respect to the number of rounds $T$. However, there is a gap of $\tilde{O}(\max(\sqrt{d}, \sqrt{k}))$ between the current best upper and lower bounds, where $d$ is the dimension of the feature vectors, $k$ is the number of the chosen arms in a round, and $\tilde{O}(\cdot)$ ignores the logarithmic factors. The dependence of $k$ and $d$ is of practical importance because $k$ may be larger than $T$ in real-world applications such as recommender systems. In this paper, we fill the gap by improving the upper and lower bounds. More precisely, we show that the C${}^2$UCB algorithm proposed by Qin, Chen, and Zhu (2014) has the optimal regret bound $\tilde{O}(d\sqrt{kT} + dk)$ for the partition matroid constraints. For general constraints, we propose an algorithm that modifies the reward estimates of arms in the C${}^2$UCB algorithm and demonstrate that it enjoys the optimal regret bound for a more general problem that can take into account other objectives simultaneously. We also show that our technique would be applicable to related problems. Numerical experiments support our theoretical results and considerations.

Approximability of Monotone Submodular Function Maximization under Cardinality and Matroid Constraints in the Streaming Model

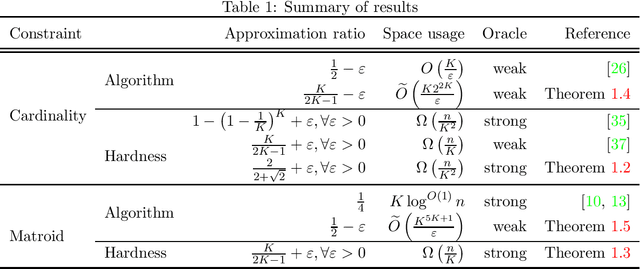
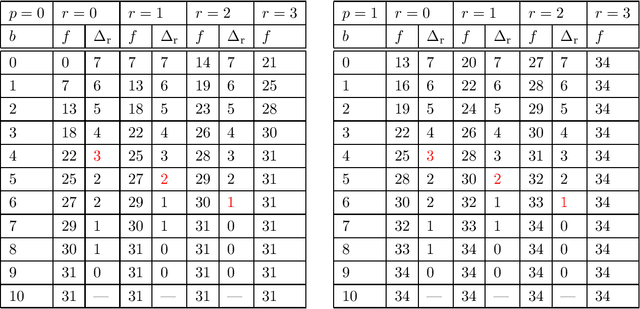
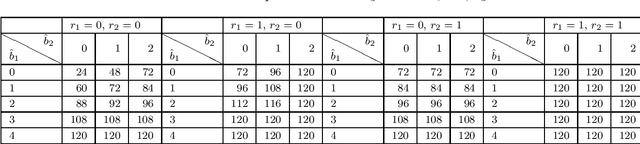
Maximizing a monotone submodular function under various constraints is a classical and intensively studied problem. However, in the single-pass streaming model, where the elements arrive one by one and an algorithm can store only a small fraction of input elements, there is much gap in our knowledge, even though several approximation algorithms have been proposed in the literature. In this work, we present the first lower bound on the approximation ratios for cardinality and matroid constraints that beat $1-\frac{1}{e}$ in the single-pass streaming model. Let $n$ be the number of elements in the stream. Then, we prove that any (randomized) streaming algorithm for a cardinality constraint with approximation ratio $\frac{2}{2+\sqrt{2}}+\varepsilon$ requires $\Omega\left(\frac{n}{K^2}\right)$ space for any $\varepsilon>0$, where $K$ is the size limit of the output set. We also prove that any (randomized) streaming algorithm for a (partition) matroid constraint with approximation ratio $\frac{K}{2K-1}+\varepsilon$ requires $\Omega\left(\frac{n}{K}\right)$ space for any $\varepsilon>0$, where $K$ is the rank of the given matroid. In addition, we give streaming algorithms when we only have a weak oracle with which we can only evaluate function values on feasible sets. Specifically, we show weak-oracle streaming algorithms for cardinality and matroid constraints with approximation ratios $\frac{K}{2K-1}$ and $\frac{1}{2}$, respectively, whose space complexity is exponential in $K$ but is independent of $n$. The former one exactly matches the known inapproximability result for a cardinality constraint in the weak oracle model. The latter one almost matches our lower bound of $\frac{K}{2K-1}$ for a matroid constraint, which almost settles the approximation ratio for a matroid constraint that can be obtained by a streaming algorithm whose space complexity is independent of $n$.

Causal Bandits with Propagating Inference

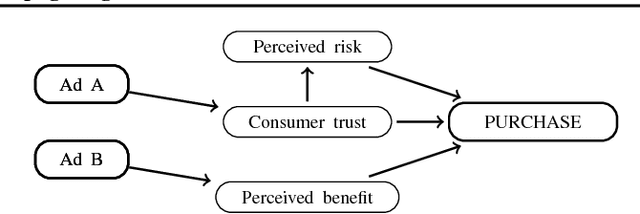
Bandit is a framework for designing sequential experiments. In each experiment, a learner selects an arm $A \in \mathcal{A}$ and obtains an observation corresponding to $A$. Theoretically, the tight regret lower-bound for the general bandit is polynomial with respect to the number of arms $|\mathcal{A}|$. This makes bandit incapable of handling an exponentially large number of arms, hence the bandit problem with side-information is often considered to overcome this lower bound. Recently, a bandit framework over a causal graph was introduced, where the structure of the causal graph is available as side-information. A causal graph is a fundamental model that is frequently used with a variety of real problems. In this setting, the arms are identified with interventions on a given causal graph, and the effect of an intervention propagates throughout all over the causal graph. The task is to find the best intervention that maximizes the expected value on a target node. Existing algorithms for causal bandit overcame the $\Omega(\sqrt{|\mathcal{A}|/T})$ simple-regret lower-bound; however, their algorithms work only when the interventions $\mathcal{A}$ are localized around a single node (i.e., an intervention propagates only to its neighbors). We propose a novel causal bandit algorithm for an arbitrary set of interventions, which can propagate throughout the causal graph. We also show that it achieves $O(\sqrt{ \gamma^*\log(|\mathcal{A}|T) / T})$ regret bound, where $\gamma^*$ is determined by using a causal graph structure. In particular, if the in-degree of the causal graph is bounded, then $\gamma^* = O(N^2)$, where $N$ is the number $N$ of nodes.