Tightly Robust Optimization via Empirical Domain Reduction

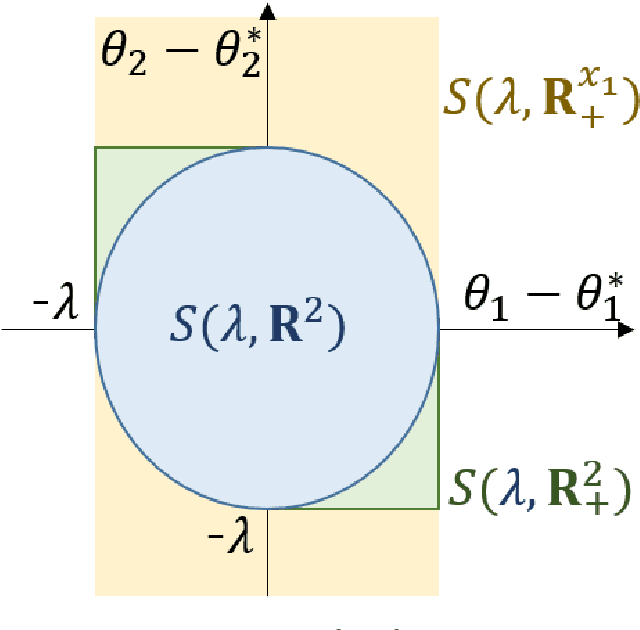
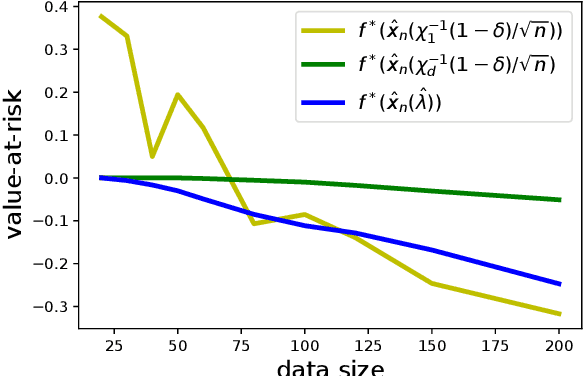
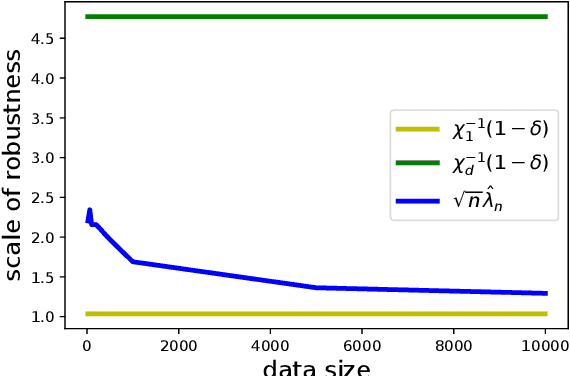
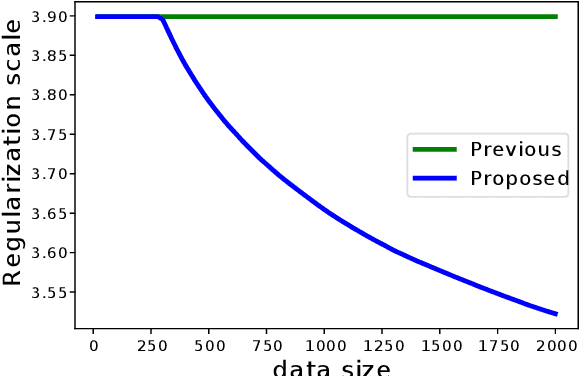
Data-driven decision-making is performed by solving a parameterized optimization problem, and the optimal decision is given by an optimal solution for unknown true parameters. We often need a solution that satisfies true constraints even though these are unknown. Robust optimization is employed to obtain such a solution, where the uncertainty of the parameter is represented by an ellipsoid, and the scale of robustness is controlled by a coefficient. In this study, we propose an algorithm to determine the scale such that the solution has a good objective value and satisfies the true constraints with a given confidence probability. Under some regularity conditions, the scale obtained by our algorithm is asymptotically $O(1/\sqrt{n})$, whereas the scale obtained by a standard approach is $O(\sqrt{d/n})$. This means that our algorithm is less affected by the dimensionality of the parameters.

Causality and Robust Optimization

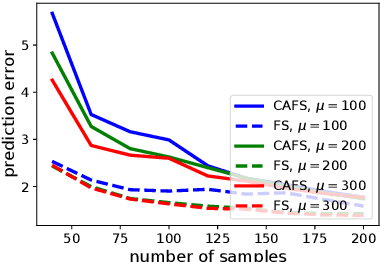
A decision-maker must consider cofounding bias when attempting to apply machine learning prediction, and, while feature selection is widely recognized as important process in data-analysis, it could cause cofounding bias. A causal Bayesian network is a standard tool for describing causal relationships, and if relationships are known, then adjustment criteria can determine with which features cofounding bias disappears. A standard modification would thus utilize causal discovery algorithms for preventing cofounding bias in feature selection. Causal discovery algorithms, however, essentially rely on the faithfulness assumption, which turn out to be easily violated in practical feature selection settings. In this paper, we propose a meta-algorithm that can remedy existing feature selection algorithms in terms of cofounding bias. Our algorithm is induced from a novel adjustment criterion that requires rather than faithfulness, an assumption which can be induced from another well-known assumption of the causal sufficiency. We further prove that the features added through our modification convert cofounding bias into prediction variance. With the aid of existing robust optimization technologies that regularize risky strategies with high variance, then, we are able to successfully improve the throughput performance of decision-making optimization, as is shown in our experimental results.

Empirical Hypothesis Space Reduction

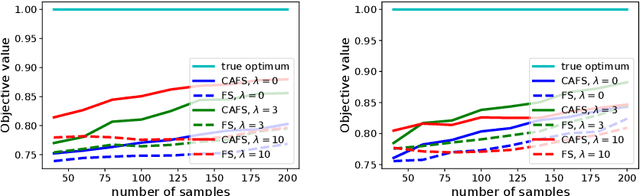
Selecting appropriate regularization coefficients is critical to performance with respect to regularized empirical risk minimization problems. Existing theoretical approaches attempt to determine the coefficients in order for regularized empirical objectives to be upper-bounds of true objectives, uniformly over a hypothesis space. Such an approach is, however, known to be over-conservative, especially in high-dimensional settings with large hypothesis space. In fact, an existing generalization error bound in variance-based regularization is $O(\sqrt{d \log n/n})$, where $d$ is the dimension of hypothesis space, and thus the number of samples required for convergence linearly increases with respect to $d$. This paper proposes an algorithm that calculates regularization coefficient, one which results in faster convergence of generalization error $O(\sqrt{\log n/n})$ and whose leading term is independent of the dimension $d$. This faster convergence without dependence on the size of the hypothesis space is achieved by means of empirical hypothesis space reduction, which, with high probability, successfully reduces a hypothesis space without losing the true optimum solution. Calculation of uniform upper bounds over reduced spaces, then, enables acceleration of the convergence of generalization error.

Causal Bandits with Propagating Inference

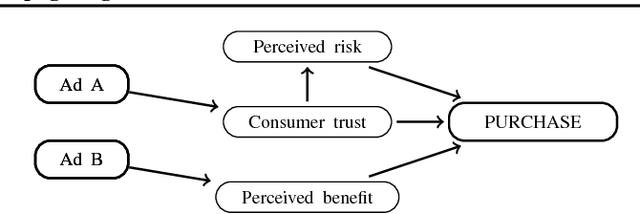
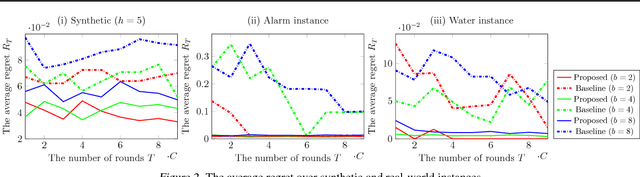
Bandit is a framework for designing sequential experiments. In each experiment, a learner selects an arm $A \in \mathcal{A}$ and obtains an observation corresponding to $A$. Theoretically, the tight regret lower-bound for the general bandit is polynomial with respect to the number of arms $|\mathcal{A}|$. This makes bandit incapable of handling an exponentially large number of arms, hence the bandit problem with side-information is often considered to overcome this lower bound. Recently, a bandit framework over a causal graph was introduced, where the structure of the causal graph is available as side-information. A causal graph is a fundamental model that is frequently used with a variety of real problems. In this setting, the arms are identified with interventions on a given causal graph, and the effect of an intervention propagates throughout all over the causal graph. The task is to find the best intervention that maximizes the expected value on a target node. Existing algorithms for causal bandit overcame the $\Omega(\sqrt{|\mathcal{A}|/T})$ simple-regret lower-bound; however, their algorithms work only when the interventions $\mathcal{A}$ are localized around a single node (i.e., an intervention propagates only to its neighbors). We propose a novel causal bandit algorithm for an arbitrary set of interventions, which can propagate throughout the causal graph. We also show that it achieves $O(\sqrt{ \gamma^*\log(|\mathcal{A}|T) / T})$ regret bound, where $\gamma^*$ is determined by using a causal graph structure. In particular, if the in-degree of the causal graph is bounded, then $\gamma^* = O(N^2)$, where $N$ is the number $N$ of nodes.