Tightly Robust Optimization via Empirical Domain Reduction
Paper and Code
Feb 29, 2020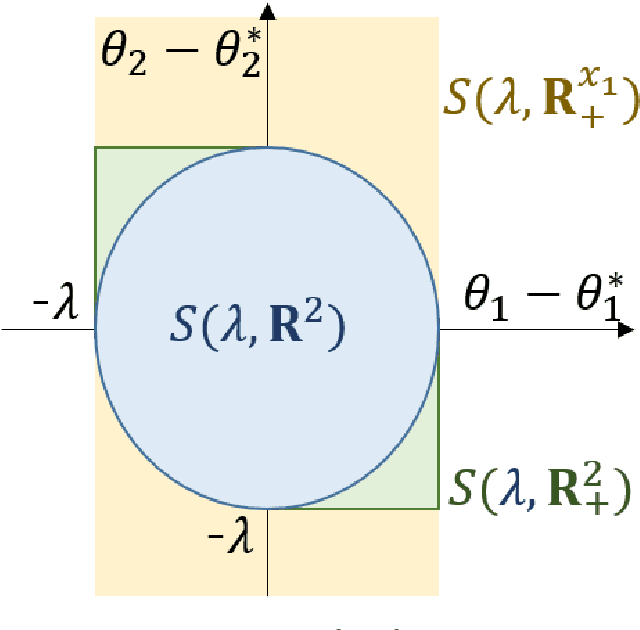
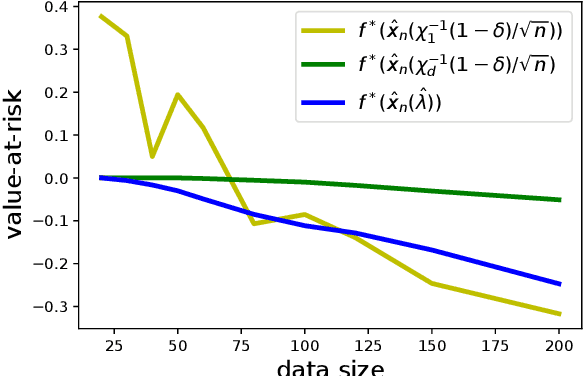
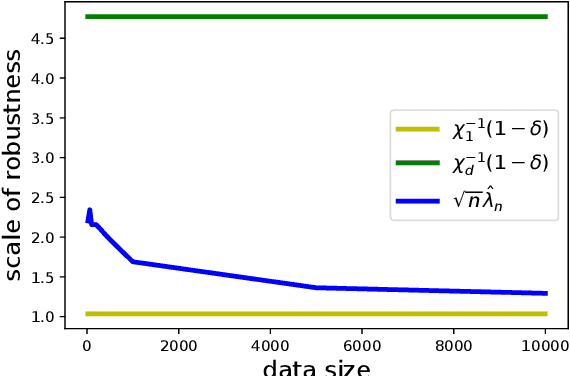
Data-driven decision-making is performed by solving a parameterized optimization problem, and the optimal decision is given by an optimal solution for unknown true parameters. We often need a solution that satisfies true constraints even though these are unknown. Robust optimization is employed to obtain such a solution, where the uncertainty of the parameter is represented by an ellipsoid, and the scale of robustness is controlled by a coefficient. In this study, we propose an algorithm to determine the scale such that the solution has a good objective value and satisfies the true constraints with a given confidence probability. Under some regularity conditions, the scale obtained by our algorithm is asymptotically $O(1/\sqrt{n})$, whereas the scale obtained by a standard approach is $O(\sqrt{d/n})$. This means that our algorithm is less affected by the dimensionality of the parameters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge