Self-Supervised Pretraining for Heterogeneous Hypergraph Neural Networks

Recently, pretraining methods for the Graph Neural Networks (GNNs) have been successful at learning effective representations from unlabeled graph data. However, most of these methods rely on pairwise relations in the graph and do not capture the underling higher-order relations between entities. Hypergraphs are versatile and expressive structures that can effectively model higher-order relationships among entities in the data. Despite the efforts to adapt GNNs to hypergraphs (HyperGNN), there are currently no fully self-supervised pretraining methods for HyperGNN on heterogeneous hypergraphs. In this paper, we present SPHH, a novel self-supervised pretraining framework for heterogeneous HyperGNNs. Our method is able to effectively capture higher-order relations among entities in the data in a self-supervised manner. SPHH is consist of two self-supervised pretraining tasks that aim to simultaneously learn both local and global representations of the entities in the hypergraph by using informative representations derived from the hypergraph structure. Overall, our work presents a significant advancement in the field of self-supervised pretraining of HyperGNNs, and has the potential to improve the performance of various graph-based downstream tasks such as node classification and link prediction tasks which are mapped to hypergraph configuration. Our experiments on two real-world benchmarks using four different HyperGNN models show that our proposed SPHH framework consistently outperforms state-of-the-art baselines in various downstream tasks. The results demonstrate that SPHH is able to improve the performance of various HyperGNN models in various downstream tasks, regardless of their architecture or complexity, which highlights the robustness of our framework.

Learning on Random Balls is Sufficient for Estimating Graph Parameters

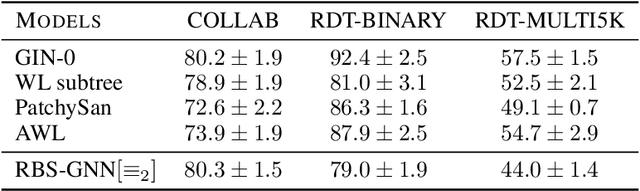
Theoretical analyses for graph learning methods often assume a complete observation of the input graph. Such an assumption might not be useful for handling any-size graphs due to the scalability issues in practice. In this work, we develop a theoretical framework for graph classification problems in the partial observation setting (i.e., subgraph samplings). Equipped with insights from graph limit theory, we propose a new graph classification model that works on a randomly sampled subgraph and a novel topology to characterize the representability of the model. Our theoretical framework contributes a theoretical validation of mini-batch learning on graphs and leads to new learning-theoretic results on generalization bounds as well as size-generalizability without assumptions on the input.

Abelian Neural Networks

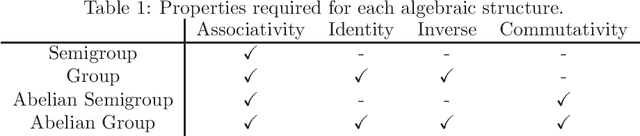
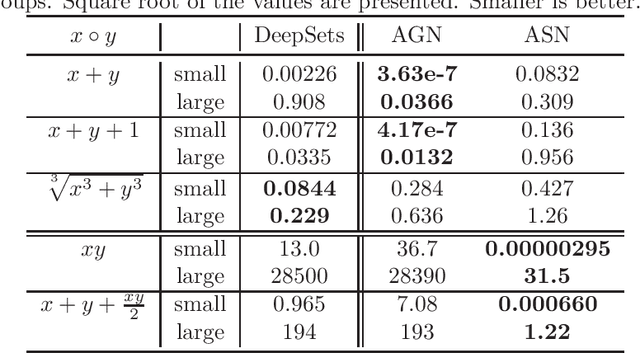
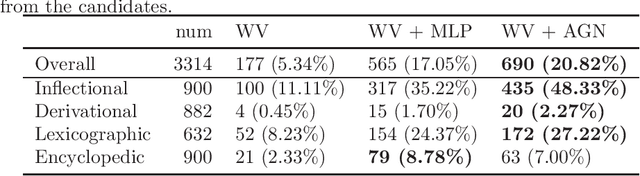
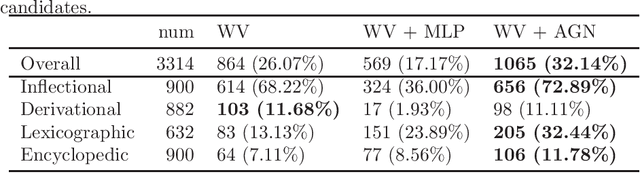
We study the problem of modeling a binary operation that satisfies some algebraic requirements. We first construct a neural network architecture for Abelian group operations and derive a universal approximation property. Then, we extend it to Abelian semigroup operations using the characterization of associative symmetric polynomials. Both models take advantage of the analytic invertibility of invertible neural networks. For each case, by repeating the binary operations, we can represent a function for multiset input thanks to the algebraic structure. Naturally, our multiset architecture has size-generalization ability, which has not been obtained in existing methods. Further, we present modeling the Abelian group operation itself is useful in a word analogy task. We train our models over fixed word embeddings and demonstrate improved performance over the original word2vec and another naive learning method.

Stacked Graph Filter

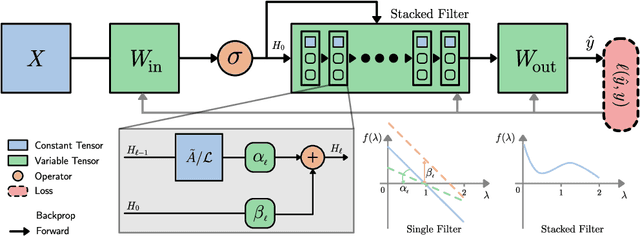
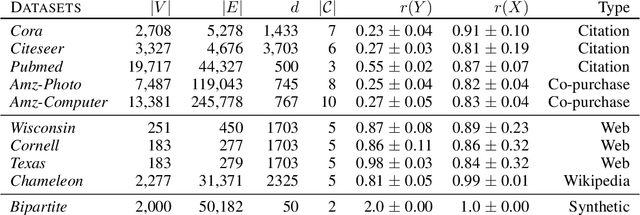
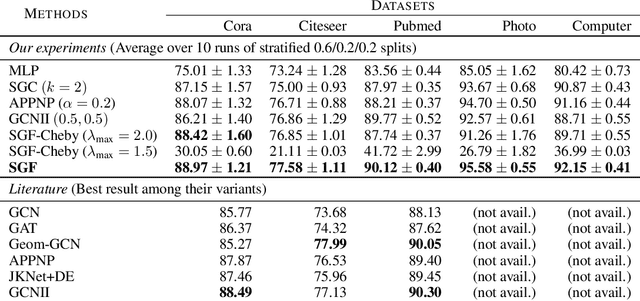
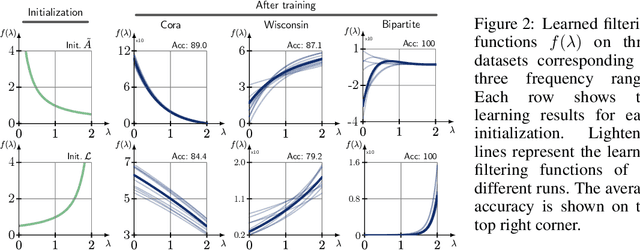
We study Graph Convolutional Networks (GCN) from the graph signal processing viewpoint by addressing a difference between learning graph filters with fully connected weights versus trainable polynomial coefficients. We find that by stacking graph filters with learnable polynomial parameters, we can build a highly adaptive and robust vertex classification model. Our treatment here relaxes the low-frequency (or equivalently, high homophily) assumptions in existing vertex classification models, resulting a more ubiquitous solution in terms of spectral properties. Empirically, by using only one hyper-parameter setting, our model achieves strong results on most benchmark datasets across the frequency spectrum.

Graph Homomorphism Convolution

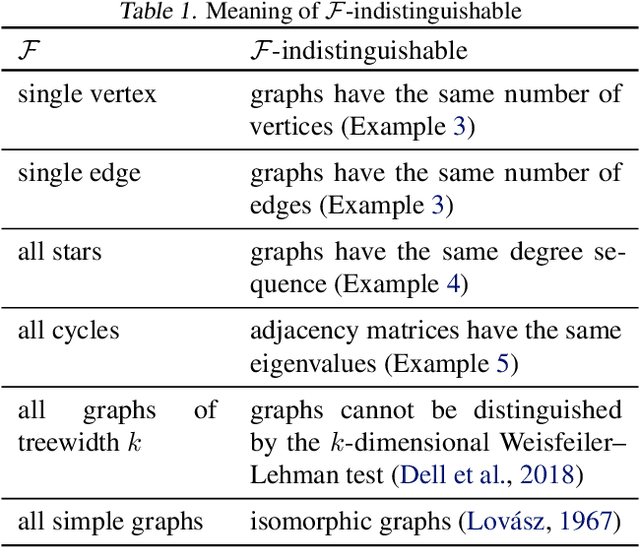
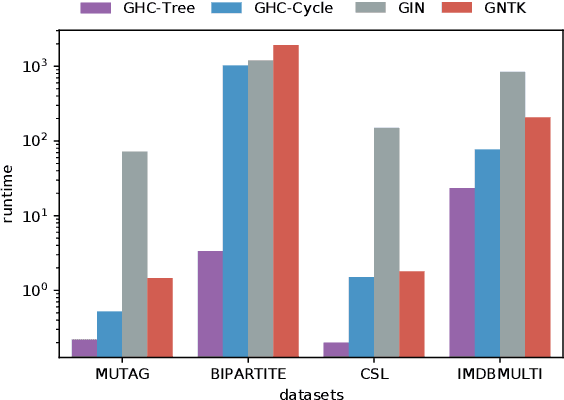
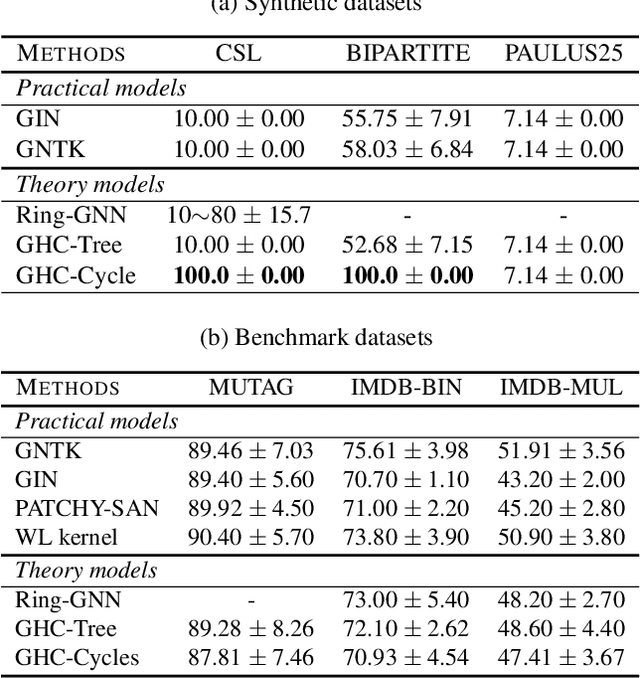
In this paper, we study the graph classification problem from the graph homomorphism perspective. We consider the homomorphisms from $F$ to $G$, where $G$ is a graph of interest (e.g. molecules or social networks) and $F$ belongs to some family of graphs (e.g. paths or non-isomorphic trees). We prove that graph homomorphism numbers provide a natural universally invariant (isomorphism invariant) embedding maps which can be used for graph classifications. In practice, by choosing $F$ to have bounded tree-width, we show that the homomorphism method is not only competitive in classification accuracy but also run much faster than other state-of-the-art methods. Finally, based on our theoretical analysis, we propose the Graph Homomorphism Convolution module which has promising performance in the graph classification task.

Tightly Robust Optimization via Empirical Domain Reduction

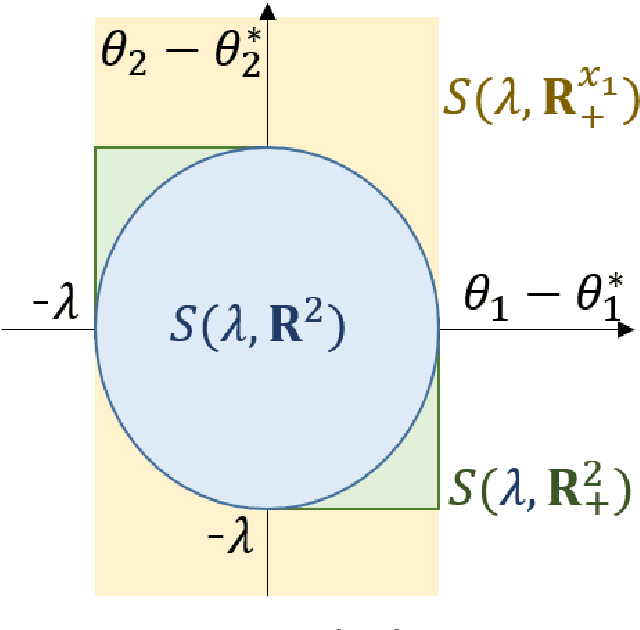
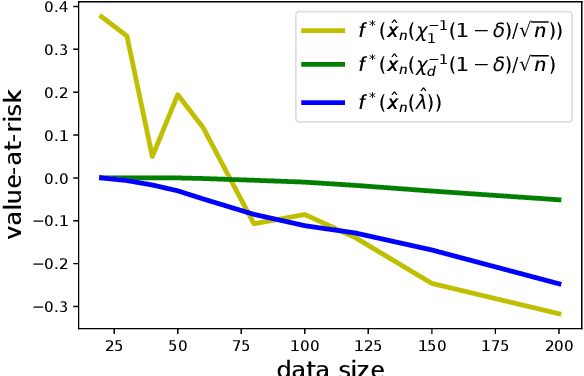
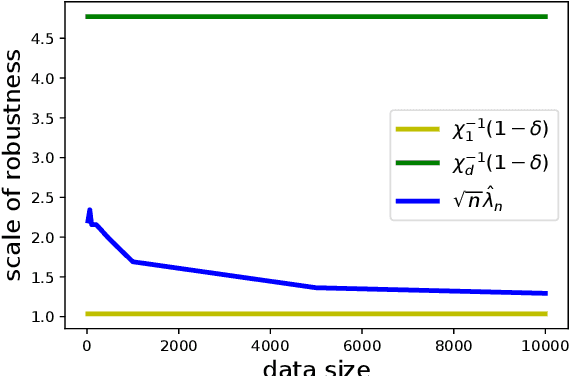
Data-driven decision-making is performed by solving a parameterized optimization problem, and the optimal decision is given by an optimal solution for unknown true parameters. We often need a solution that satisfies true constraints even though these are unknown. Robust optimization is employed to obtain such a solution, where the uncertainty of the parameter is represented by an ellipsoid, and the scale of robustness is controlled by a coefficient. In this study, we propose an algorithm to determine the scale such that the solution has a good objective value and satisfies the true constraints with a given confidence probability. Under some regularity conditions, the scale obtained by our algorithm is asymptotically $O(1/\sqrt{n})$, whereas the scale obtained by a standard approach is $O(\sqrt{d/n})$. This means that our algorithm is less affected by the dimensionality of the parameters.

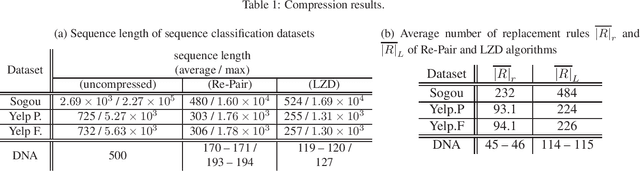
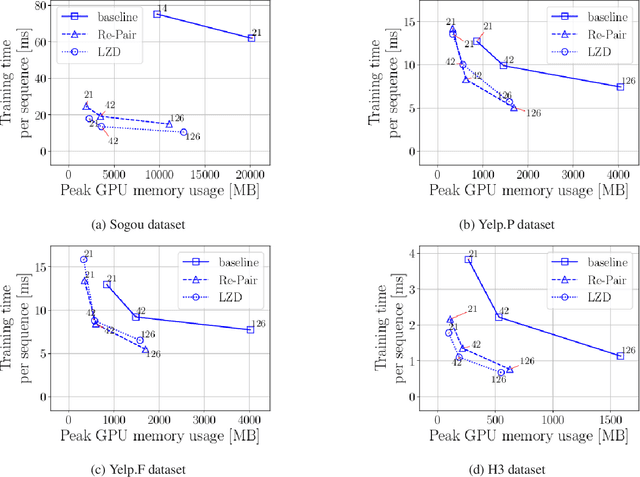
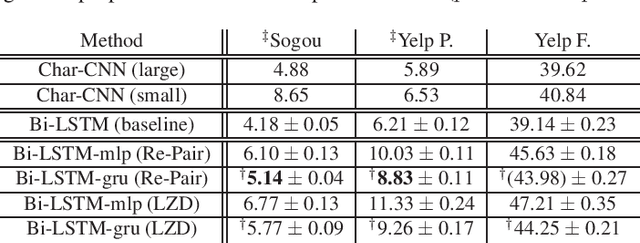
Learning Directly from Grammar Compressed Text

Neural networks using numerous text data have been successfully applied to a variety of tasks. While massive text data is usually compressed using techniques such as grammar compression, almost all of the previous machine learning methods assume already decompressed sequence data as their input. In this paper, we propose a method to directly apply neural sequence models to text data compressed with grammar compression algorithms without decompression. To encode the unique symbols that appear in compression rules, we introduce composer modules to incrementally encode the symbols into vector representations. Through experiments on real datasets, we empirically showed that the proposal model can achieve both memory and computational efficiency while maintaining moderate performance.

A Simple Proof of the Universality of Invariant/Equivariant Graph Neural Networks

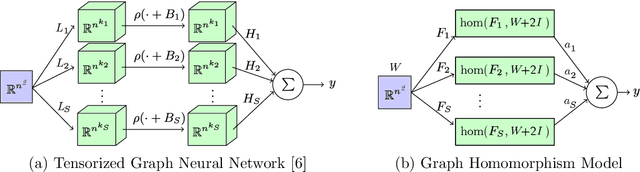
We present a simple proof for the universality of invariant and equivariant tensorized graph neural networks. Our approach considers a restricted intermediate hypothetical model named Graph Homomorphism Model to reach the universality conclusions including an open case for higher-order output. We find that our proposed technique not only leads to simple proofs of the universality properties but also gives a natural explanation for the tensorization of the previously studied models. Finally, we give some remarks on the connection between our model and the continuous representation of graphs.

Empirical Hypothesis Space Reduction

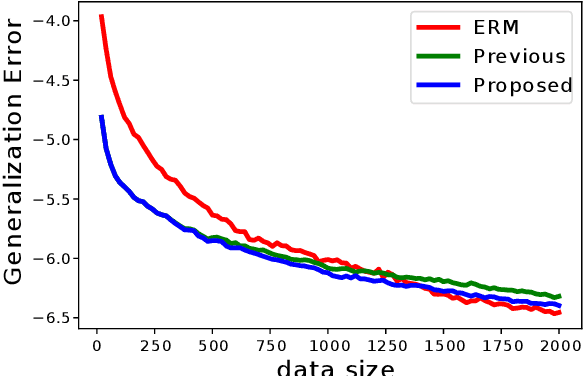
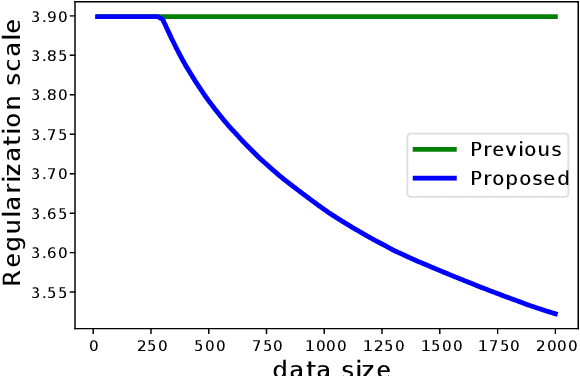
Selecting appropriate regularization coefficients is critical to performance with respect to regularized empirical risk minimization problems. Existing theoretical approaches attempt to determine the coefficients in order for regularized empirical objectives to be upper-bounds of true objectives, uniformly over a hypothesis space. Such an approach is, however, known to be over-conservative, especially in high-dimensional settings with large hypothesis space. In fact, an existing generalization error bound in variance-based regularization is $O(\sqrt{d \log n/n})$, where $d$ is the dimension of hypothesis space, and thus the number of samples required for convergence linearly increases with respect to $d$. This paper proposes an algorithm that calculates regularization coefficient, one which results in faster convergence of generalization error $O(\sqrt{\log n/n})$ and whose leading term is independent of the dimension $d$. This faster convergence without dependence on the size of the hypothesis space is achieved by means of empirical hypothesis space reduction, which, with high probability, successfully reduces a hypothesis space without losing the true optimum solution. Calculation of uniform upper bounds over reduced spaces, then, enables acceleration of the convergence of generalization error.

Data Cleansing for Models Trained with SGD

Data cleansing is a typical approach used to improve the accuracy of machine learning models, which, however, requires extensive domain knowledge to identify the influential instances that affect the models. In this paper, we propose an algorithm that can suggest influential instances without using any domain knowledge. With the proposed method, users only need to inspect the instances suggested by the algorithm, implying that users do not need extensive knowledge for this procedure, which enables even non-experts to conduct data cleansing and improve the model. The existing methods require the loss function to be convex and an optimal model to be obtained, which is not always the case in modern machine learning. To overcome these limitations, we propose a novel approach specifically designed for the models trained with stochastic gradient descent (SGD). The proposed method infers the influential instances by retracing the steps of the SGD while incorporating intermediate models computed in each step. Through experiments, we demonstrate that the proposed method can accurately infer the influential instances. Moreover, we used MNIST and CIFAR10 to show that the models can be effectively improved by removing the influential instances suggested by the proposed method.