Graph Homomorphism Convolution
Paper and Code
May 03, 2020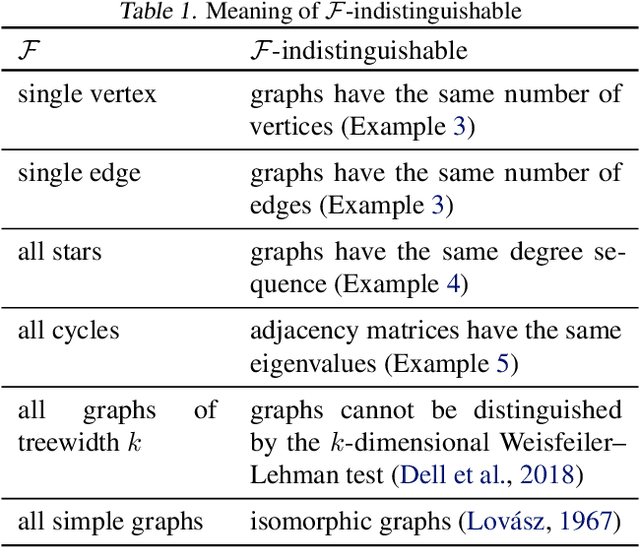
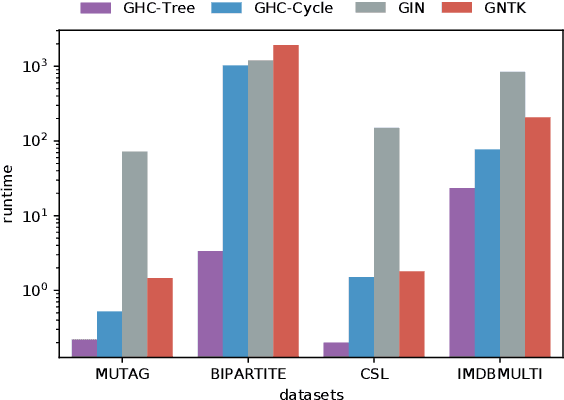
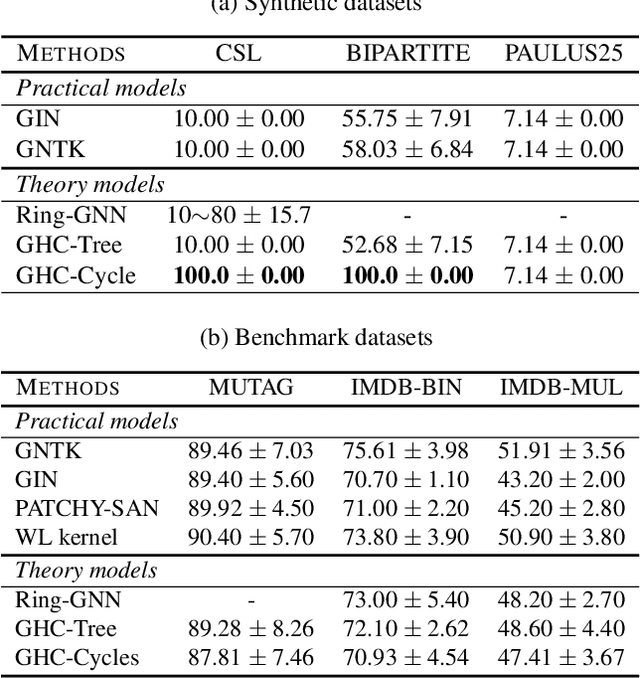

In this paper, we study the graph classification problem from the graph homomorphism perspective. We consider the homomorphisms from $F$ to $G$, where $G$ is a graph of interest (e.g. molecules or social networks) and $F$ belongs to some family of graphs (e.g. paths or non-isomorphic trees). We prove that graph homomorphism numbers provide a natural universally invariant (isomorphism invariant) embedding maps which can be used for graph classifications. In practice, by choosing $F$ to have bounded tree-width, we show that the homomorphism method is not only competitive in classification accuracy but also run much faster than other state-of-the-art methods. Finally, based on our theoretical analysis, we propose the Graph Homomorphism Convolution module which has promising performance in the graph classification task.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge