Leaping Through Time with Gradient-based Adaptation for Recommendation

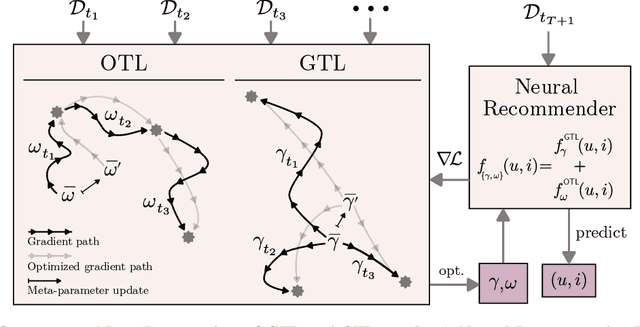
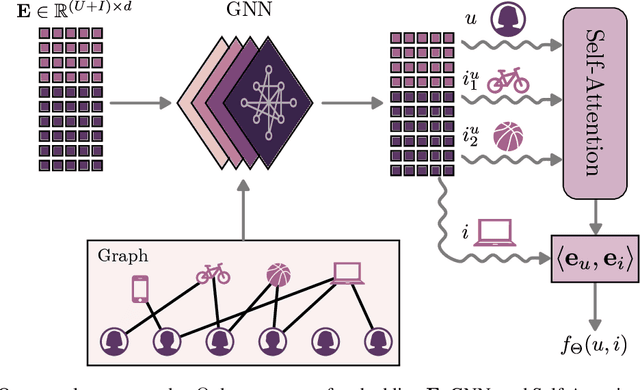
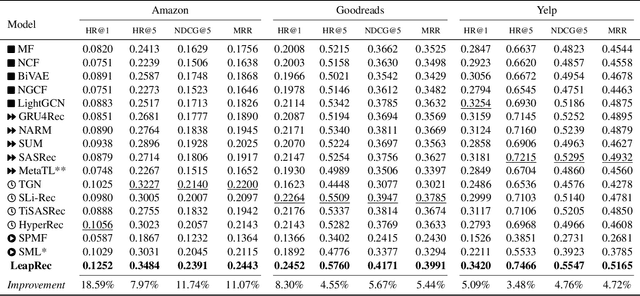
Modern recommender systems are required to adapt to the change in user preferences and item popularity. Such a problem is known as the temporal dynamics problem, and it is one of the main challenges in recommender system modeling. Different from the popular recurrent modeling approach, we propose a new solution named LeapRec to the temporal dynamic problem by using trajectory-based meta-learning to model time dependencies. LeapRec characterizes temporal dynamics by two complement components named global time leap (GTL) and ordered time leap (OTL). By design, GTL learns long-term patterns by finding the shortest learning path across unordered temporal data. Cooperatively, OTL learns short-term patterns by considering the sequential nature of the temporal data. Our experimental results show that LeapRec consistently outperforms the state-of-the-art methods on several datasets and recommendation metrics. Furthermore, we provide an empirical study of the interaction between GTL and OTL, showing the effects of long- and short-term modeling.

Learning on Random Balls is Sufficient for Estimating Graph Parameters

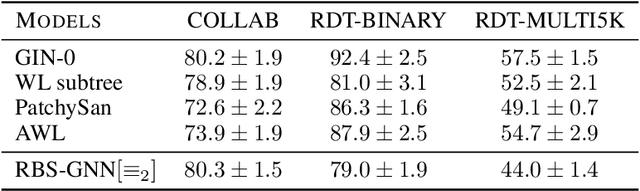
Theoretical analyses for graph learning methods often assume a complete observation of the input graph. Such an assumption might not be useful for handling any-size graphs due to the scalability issues in practice. In this work, we develop a theoretical framework for graph classification problems in the partial observation setting (i.e., subgraph samplings). Equipped with insights from graph limit theory, we propose a new graph classification model that works on a randomly sampled subgraph and a novel topology to characterize the representability of the model. Our theoretical framework contributes a theoretical validation of mini-batch learning on graphs and leads to new learning-theoretic results on generalization bounds as well as size-generalizability without assumptions on the input.

Stacked Graph Filter

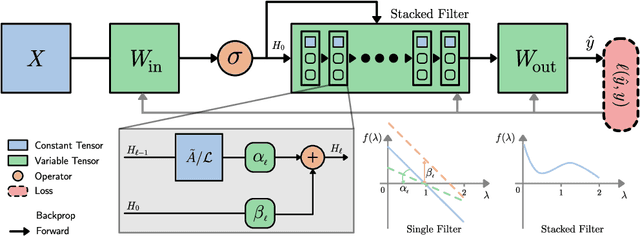
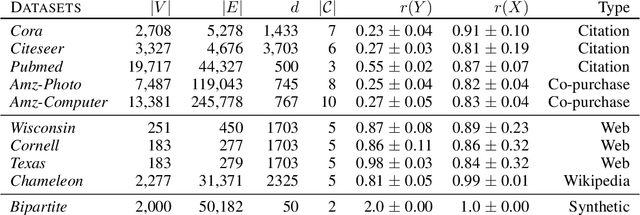
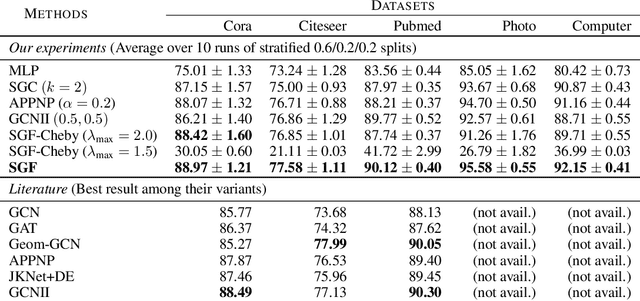
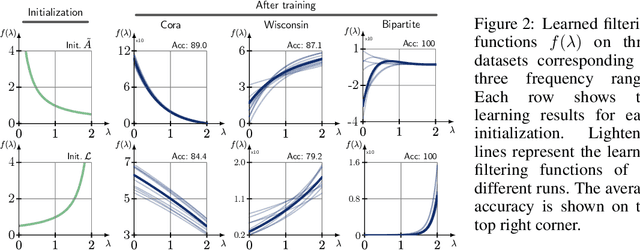
We study Graph Convolutional Networks (GCN) from the graph signal processing viewpoint by addressing a difference between learning graph filters with fully connected weights versus trainable polynomial coefficients. We find that by stacking graph filters with learnable polynomial parameters, we can build a highly adaptive and robust vertex classification model. Our treatment here relaxes the low-frequency (or equivalently, high homophily) assumptions in existing vertex classification models, resulting a more ubiquitous solution in terms of spectral properties. Empirically, by using only one hyper-parameter setting, our model achieves strong results on most benchmark datasets across the frequency spectrum.

Graph Homomorphism Convolution

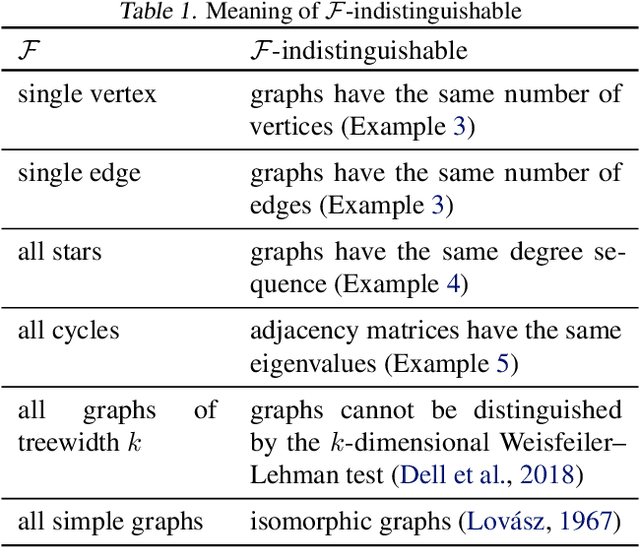
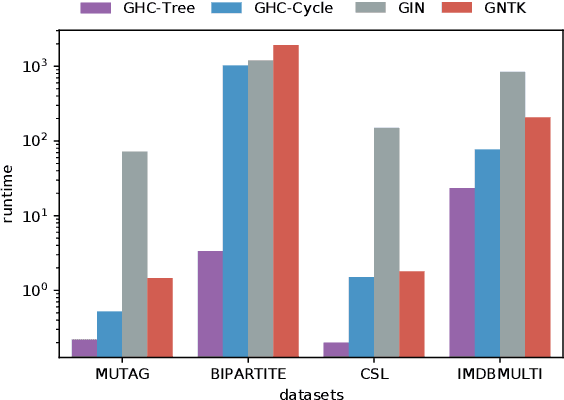
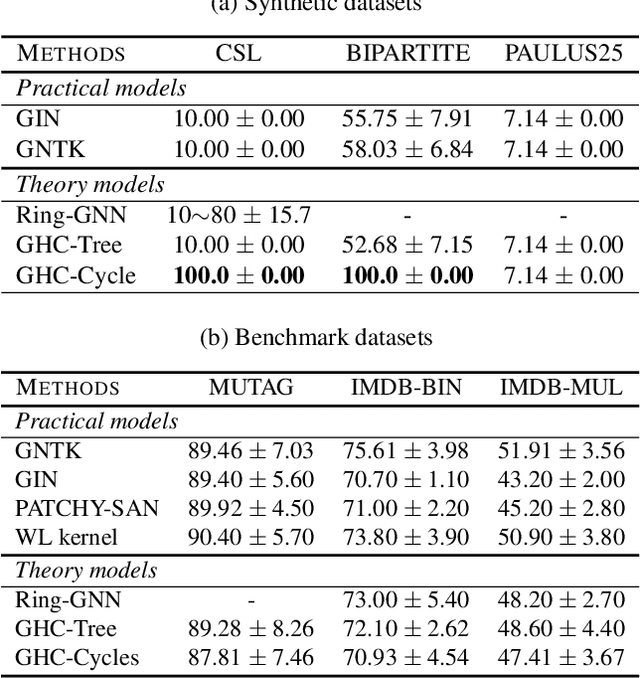
In this paper, we study the graph classification problem from the graph homomorphism perspective. We consider the homomorphisms from $F$ to $G$, where $G$ is a graph of interest (e.g. molecules or social networks) and $F$ belongs to some family of graphs (e.g. paths or non-isomorphic trees). We prove that graph homomorphism numbers provide a natural universally invariant (isomorphism invariant) embedding maps which can be used for graph classifications. In practice, by choosing $F$ to have bounded tree-width, we show that the homomorphism method is not only competitive in classification accuracy but also run much faster than other state-of-the-art methods. Finally, based on our theoretical analysis, we propose the Graph Homomorphism Convolution module which has promising performance in the graph classification task.

A Simple Proof of the Universality of Invariant/Equivariant Graph Neural Networks

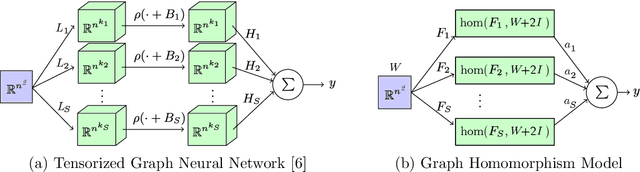
We present a simple proof for the universality of invariant and equivariant tensorized graph neural networks. Our approach considers a restricted intermediate hypothetical model named Graph Homomorphism Model to reach the universality conclusions including an open case for higher-order output. We find that our proposed technique not only leads to simple proofs of the universality properties but also gives a natural explanation for the tensorization of the previously studied models. Finally, we give some remarks on the connection between our model and the continuous representation of graphs.

Revisiting Graph Neural Networks: All We Have is Low-Pass Filters

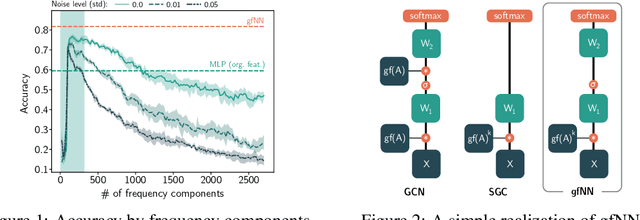
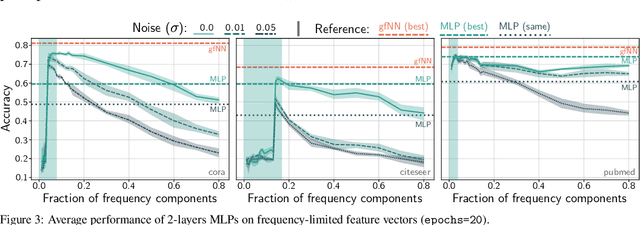
Graph neural networks have become one of the most important techniques to solve machine learning problems on graph-structured data. Recent work on vertex classification proposed deep and distributed learning models to achieve high performance and scalability. However, we find that the feature vectors of benchmark datasets are already quite informative for the classification task, and the graph structure only provides a means to denoise the data. In this paper, we develop a theoretical framework based on graph signal processing for analyzing graph neural networks. Our results indicate that graph neural networks only perform low-pass filtering on feature vectors and do not have the non-linear manifold learning property. We further investigate their resilience to feature noise and propose some insights on GCN-based graph neural network design.

Learning Graph Neural Networks with Noisy Labels

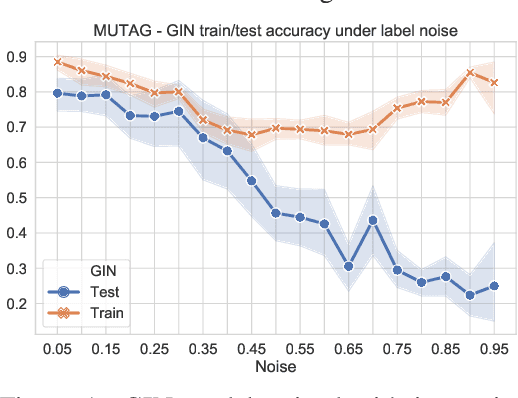
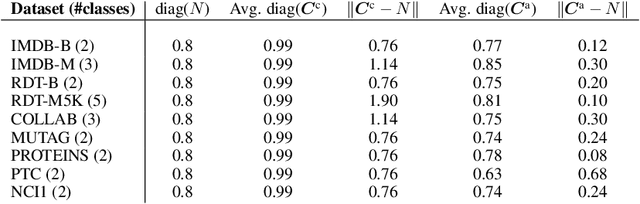
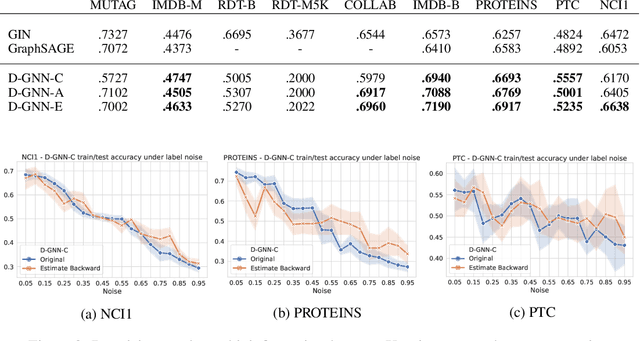
We study the robustness to symmetric label noise of GNNs training procedures. By combining the nonlinear neural message-passing models (e.g. Graph Isomorphism Networks, GraphSAGE, etc.) with loss correction methods, we present a noise-tolerant approach for the graph classification task. Our experiments show that test accuracy can be improved under the artificial symmetric noisy setting.