Stacked Graph Filter
Paper and Code
Nov 22, 2020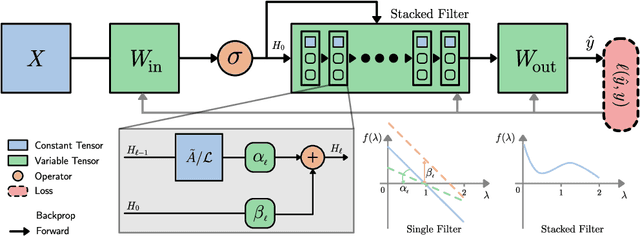
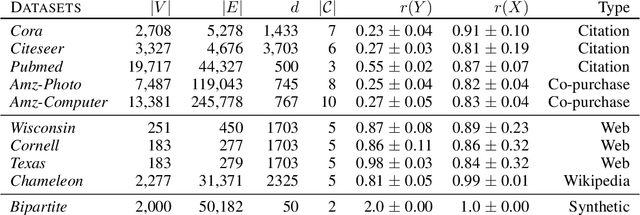
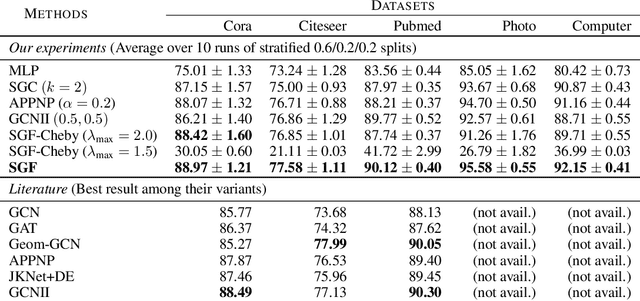
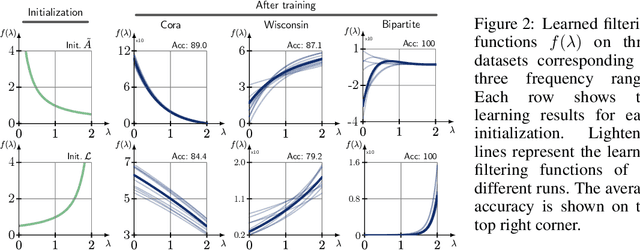
We study Graph Convolutional Networks (GCN) from the graph signal processing viewpoint by addressing a difference between learning graph filters with fully connected weights versus trainable polynomial coefficients. We find that by stacking graph filters with learnable polynomial parameters, we can build a highly adaptive and robust vertex classification model. Our treatment here relaxes the low-frequency (or equivalently, high homophily) assumptions in existing vertex classification models, resulting a more ubiquitous solution in terms of spectral properties. Empirically, by using only one hyper-parameter setting, our model achieves strong results on most benchmark datasets across the frequency spectrum.
* Source code is provided at github.com/gear/sgf
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge