PLaMo-100B: A Ground-Up Language Model Designed for Japanese Proficiency

We introduce PLaMo-100B, a large-scale language model designed for Japanese proficiency. The model was trained from scratch using 2 trillion tokens, with architecture such as QK Normalization and Z-Loss to ensure training stability during the training process. Post-training techniques, including Supervised Fine-Tuning and Direct Preference Optimization, were applied to refine the model's performance. Benchmark evaluations suggest that PLaMo-100B performs well, particularly in Japanese-specific tasks, achieving results that are competitive with frontier models like GPT-4.

Abelian Neural Networks

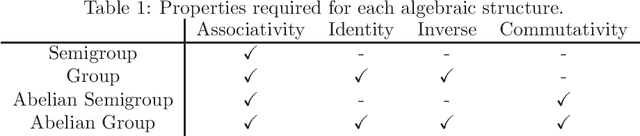
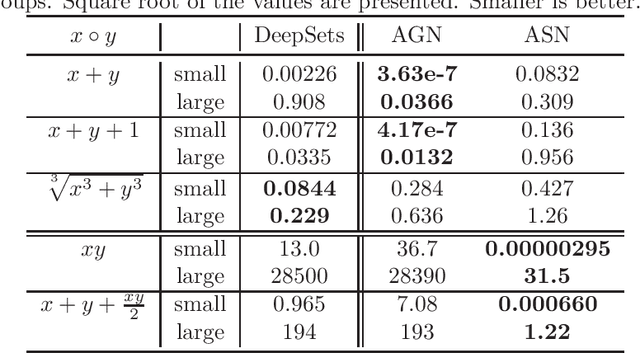
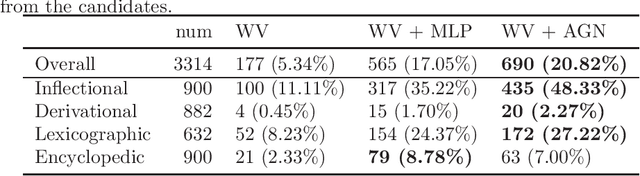
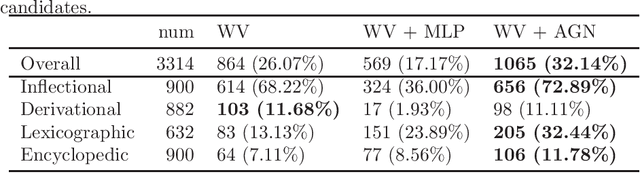
We study the problem of modeling a binary operation that satisfies some algebraic requirements. We first construct a neural network architecture for Abelian group operations and derive a universal approximation property. Then, we extend it to Abelian semigroup operations using the characterization of associative symmetric polynomials. Both models take advantage of the analytic invertibility of invertible neural networks. For each case, by repeating the binary operations, we can represent a function for multiset input thanks to the algebraic structure. Naturally, our multiset architecture has size-generalization ability, which has not been obtained in existing methods. Further, we present modeling the Abelian group operation itself is useful in a word analogy task. We train our models over fixed word embeddings and demonstrate improved performance over the original word2vec and another naive learning method.

Solving NP-Hard Problems on Graphs by Reinforcement Learning without Domain Knowledge

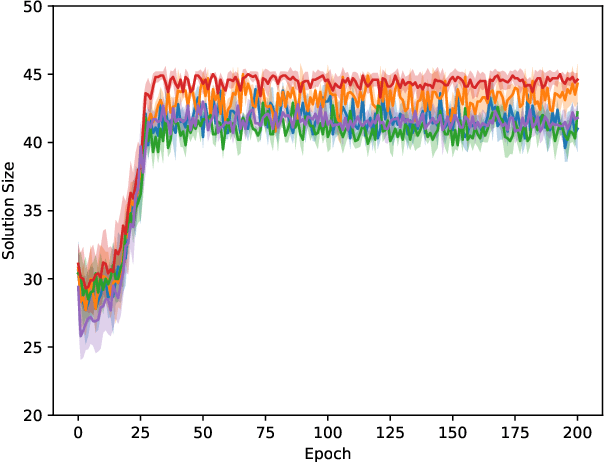
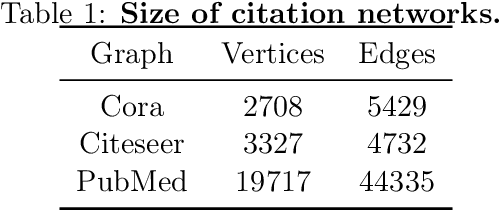
We propose an algorithm based on reinforcement learning for solving NP-hard problems on graphs. We combine Graph Isomorphism Networks and the Monte-Carlo Tree Search, which was originally used for game searches, for solving combinatorial optimization on graphs. Similarly to AlphaGo Zero, our method does not require any problem-specific knowledge or labeled datasets (exact solutions), which are difficult to calculate in principle. We show that our method, which is trained by generated random graphs, successfully finds near-optimal solutions for the Maximum Independent Set problem on citation networks. Experiments illustrate that the performance of our method is comparable to SOTA solvers, but we do not require any problem-specific reduction rules, which is highly desirable in practice since collecting hand-crafted reduction rules is costly and not adaptive for a wide range of problems.