Causal Bandits with Propagating Inference
Paper and Code
Jun 06, 2018
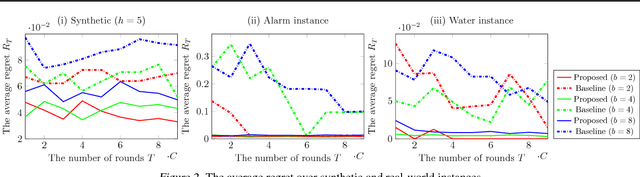
Bandit is a framework for designing sequential experiments. In each experiment, a learner selects an arm $A \in \mathcal{A}$ and obtains an observation corresponding to $A$. Theoretically, the tight regret lower-bound for the general bandit is polynomial with respect to the number of arms $|\mathcal{A}|$. This makes bandit incapable of handling an exponentially large number of arms, hence the bandit problem with side-information is often considered to overcome this lower bound. Recently, a bandit framework over a causal graph was introduced, where the structure of the causal graph is available as side-information. A causal graph is a fundamental model that is frequently used with a variety of real problems. In this setting, the arms are identified with interventions on a given causal graph, and the effect of an intervention propagates throughout all over the causal graph. The task is to find the best intervention that maximizes the expected value on a target node. Existing algorithms for causal bandit overcame the $\Omega(\sqrt{|\mathcal{A}|/T})$ simple-regret lower-bound; however, their algorithms work only when the interventions $\mathcal{A}$ are localized around a single node (i.e., an intervention propagates only to its neighbors). We propose a novel causal bandit algorithm for an arbitrary set of interventions, which can propagate throughout the causal graph. We also show that it achieves $O(\sqrt{ \gamma^*\log(|\mathcal{A}|T) / T})$ regret bound, where $\gamma^*$ is determined by using a causal graph structure. In particular, if the in-degree of the causal graph is bounded, then $\gamma^* = O(N^2)$, where $N$ is the number $N$ of nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge