Yusuke Kobayashi
Reforming an Envy-Free Matching
Jul 06, 2022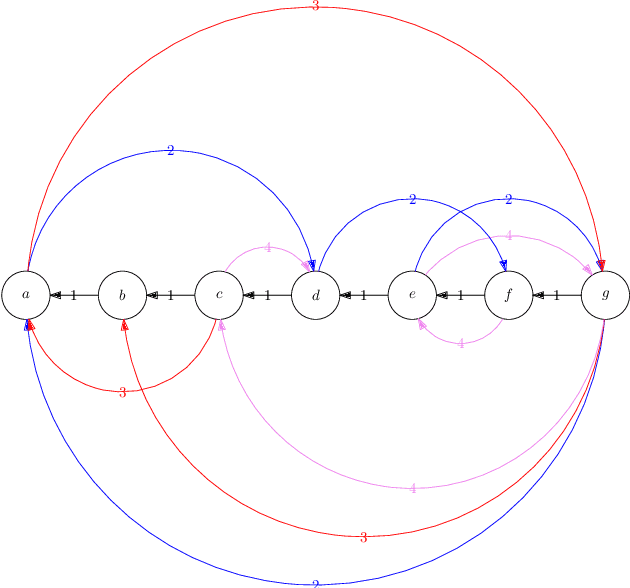
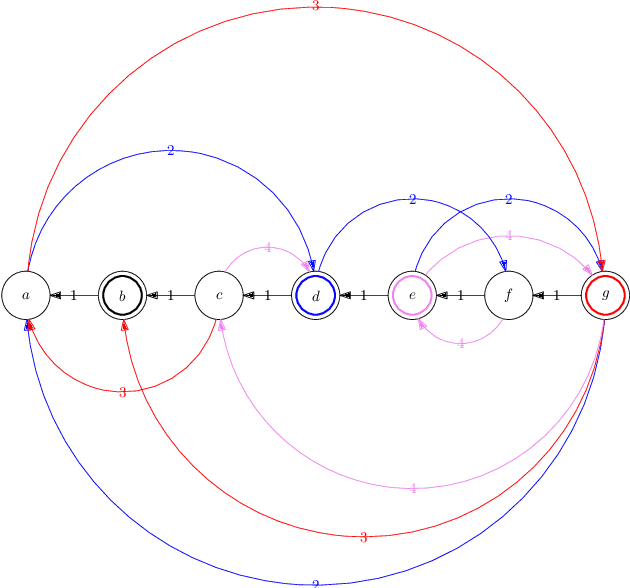
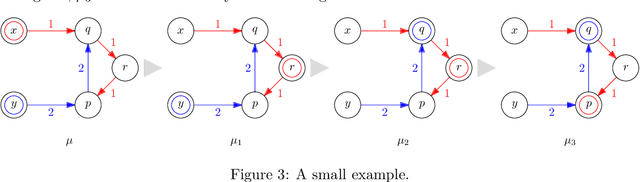
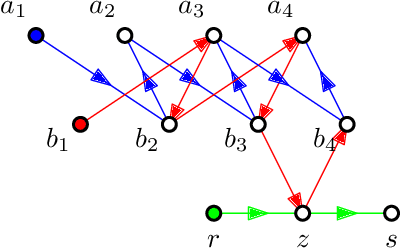
Abstract:We consider the problem of reforming an envy-free matching when each agent is assigned a single item. Given an envy-free matching, we consider an operation to exchange the item of an agent with an unassigned item preferred by the agent that results in another envy-free matching. We repeat this operation as long as we can. We prove that the resulting envy-free matching is uniquely determined up to the choice of an initial envy-free matching, and can be found in polynomial time. We call the resulting matching a reformist envy-free matching, and then we study a shortest sequence to obtain the reformist envy-free matching from an initial envy-free matching. We prove that a shortest sequence is computationally hard to obtain even when each agent accepts at most four items and each item is accepted by at most three agents. On the other hand, we give polynomial-time algorithms when each agent accepts at most three items or each item is accepted by at most two agents. Inapproximability and fixed-parameter (in)tractability are also discussed.
Fence patrolling by mobile agents with distinct speeds
Jul 30, 2014



Abstract:Suppose we want to patrol a fence (line segment) using k mobile agents with given speeds v_1, ..., v_k so that every point on the fence is visited by an agent at least once in every unit time period. Czyzowicz et al. conjectured that the maximum length of the fence that can be patrolled is (v_1 + ... + v_k)/2, which is achieved by the simple strategy where each agent i moves back and forth in a segment of length v_i/2. We disprove this conjecture by a counterexample involving k = 6 agents. We also show that the conjecture is true for k = 2, 3.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge