Stable Matching with Ties: Approximation Ratios and Learning

We study the problem of matching markets with ties, where one side of the market does not necessarily have strict preferences over members at its other side. For example, workers do not always have strict preferences over jobs, students can give the same ranking for different schools and more. In particular, assume w.l.o.g. that workers' preferences are determined by their utility from being matched to each job, which might admit ties. Notably, in contrast to classical two-sided markets with strict preferences, there is no longer a single stable matching that simultaneously maximizes the utility for all workers. We aim to guarantee each worker the largest possible share from the utility in her best possible stable matching. We call the ratio between the worker's best possible stable utility and its assigned utility the \emph{Optimal Stable Share} (OSS)-ratio. We first prove that distributions over stable matchings cannot guarantee an OSS-ratio that is sublinear in the number of workers. Instead, randomizing over possibly non-stable matchings, we show how to achieve a tight logarithmic OSS-ratio. Then, we analyze the case where the real utility is not necessarily known and can only be approximated. In particular, we provide an algorithm that guarantees a similar fraction of the utility compared to the best possible utility. Finally, we move to a bandit setting, where we select a matching at each round and only observe the utilities for matches we perform. We show how to utilize our results for approximate utilities to gracefully interpolate between problems without ties and problems with statistical ties (small suboptimality gaps).

Approximability of Monotone Submodular Function Maximization under Cardinality and Matroid Constraints in the Streaming Model

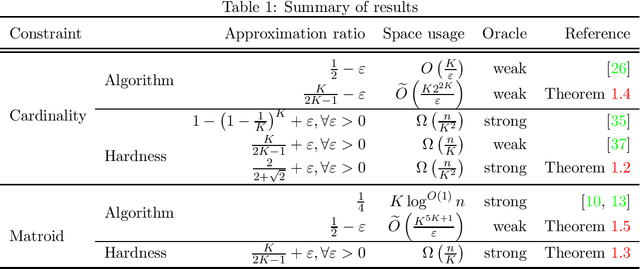
Maximizing a monotone submodular function under various constraints is a classical and intensively studied problem. However, in the single-pass streaming model, where the elements arrive one by one and an algorithm can store only a small fraction of input elements, there is much gap in our knowledge, even though several approximation algorithms have been proposed in the literature. In this work, we present the first lower bound on the approximation ratios for cardinality and matroid constraints that beat $1-\frac{1}{e}$ in the single-pass streaming model. Let $n$ be the number of elements in the stream. Then, we prove that any (randomized) streaming algorithm for a cardinality constraint with approximation ratio $\frac{2}{2+\sqrt{2}}+\varepsilon$ requires $\Omega\left(\frac{n}{K^2}\right)$ space for any $\varepsilon>0$, where $K$ is the size limit of the output set. We also prove that any (randomized) streaming algorithm for a (partition) matroid constraint with approximation ratio $\frac{K}{2K-1}+\varepsilon$ requires $\Omega\left(\frac{n}{K}\right)$ space for any $\varepsilon>0$, where $K$ is the rank of the given matroid. In addition, we give streaming algorithms when we only have a weak oracle with which we can only evaluate function values on feasible sets. Specifically, we show weak-oracle streaming algorithms for cardinality and matroid constraints with approximation ratios $\frac{K}{2K-1}$ and $\frac{1}{2}$, respectively, whose space complexity is exponential in $K$ but is independent of $n$. The former one exactly matches the known inapproximability result for a cardinality constraint in the weak oracle model. The latter one almost matches our lower bound of $\frac{K}{2K-1}$ for a matroid constraint, which almost settles the approximation ratio for a matroid constraint that can be obtained by a streaming algorithm whose space complexity is independent of $n$.