Stable Matching with Ties: Approximation Ratios and Learning

We study the problem of matching markets with ties, where one side of the market does not necessarily have strict preferences over members at its other side. For example, workers do not always have strict preferences over jobs, students can give the same ranking for different schools and more. In particular, assume w.l.o.g. that workers' preferences are determined by their utility from being matched to each job, which might admit ties. Notably, in contrast to classical two-sided markets with strict preferences, there is no longer a single stable matching that simultaneously maximizes the utility for all workers. We aim to guarantee each worker the largest possible share from the utility in her best possible stable matching. We call the ratio between the worker's best possible stable utility and its assigned utility the \emph{Optimal Stable Share} (OSS)-ratio. We first prove that distributions over stable matchings cannot guarantee an OSS-ratio that is sublinear in the number of workers. Instead, randomizing over possibly non-stable matchings, we show how to achieve a tight logarithmic OSS-ratio. Then, we analyze the case where the real utility is not necessarily known and can only be approximated. In particular, we provide an algorithm that guarantees a similar fraction of the utility compared to the best possible utility. Finally, we move to a bandit setting, where we select a matching at each round and only observe the utilities for matches we perform. We show how to utilize our results for approximate utilities to gracefully interpolate between problems without ties and problems with statistical ties (small suboptimality gaps).

abess: A Fast Best Subset Selection Library in Python and R

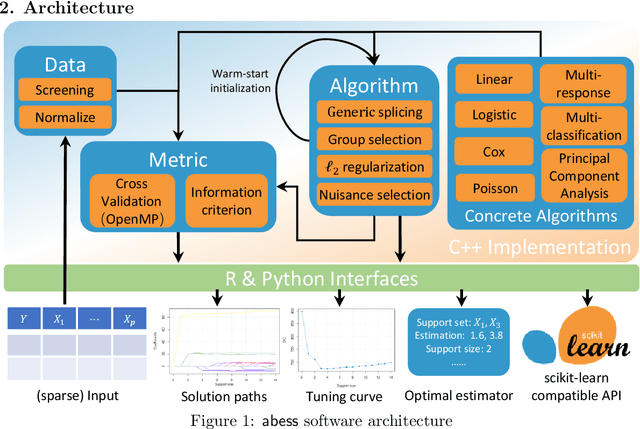
We introduce a new library named abess that implements a unified framework of best-subset selection for solving diverse machine learning problems, e.g., linear regression, classification, and principal component analysis. Particularly, the abess certifiably gets the optimal solution within polynomial times under the linear model. Our efficient implementation allows abess to attain the solution of best-subset selection problems as fast as or even 100x faster than existing competing variable (model) selection toolboxes. Furthermore, it supports common variants like best group subset selection and $\ell_2$ regularized best-subset selection. The core of the library is programmed in C++. For ease of use, a Python library is designed for conveniently integrating with scikit-learn, and it can be installed from the Python library Index. In addition, a user-friendly R library is available at the Comprehensive R Archive Network. The source code is available at: https://github.com/abess-team/abess.

Computational analysis of pathological image enables interpretable prediction for microsatellite instability

Microsatellite instability (MSI) is associated with several tumor types and its status has become increasingly vital in guiding patient treatment decisions. However, in clinical practice, distinguishing MSI from its counterpart is challenging since the diagnosis of MSI requires additional genetic or immunohistochemical tests. In this study, interpretable pathological image analysis strategies are established to help medical experts to automatically identify MSI. The strategies only require ubiquitous Haematoxylin and eosin-stained whole-slide images and can achieve decent performance in the three cohorts collected from The Cancer Genome Atlas. The strategies provide interpretability in two aspects. On the one hand, the image-level interpretability is achieved by generating localization heat maps of important regions based on the deep learning network; on the other hand, the feature-level interpretability is attained through feature importance and pathological feature interaction analysis. More interestingly, both from the image-level and feature-level interpretability, color features and texture characteristics are shown to contribute the most to the MSI predictions. Therefore, the classification models under the proposed strategies can not only serve as an efficient tool for predicting the MSI status of patients, but also provide more insights to pathologists with clinical understanding.