Sparse Equation Matching: A Derivative-Free Learning for General-Order Dynamical Systems

Equation discovery is a fundamental learning task for uncovering the underlying dynamics of complex systems, with wide-ranging applications in areas such as brain connectivity analysis, climate modeling, gene regulation, and physical system simulation. However, many existing approaches rely on accurate derivative estimation and are limited to first-order dynamical systems, restricting their applicability to real-world scenarios. In this work, we propose sparse equation matching (SEM), a unified framework that encompasses several existing equation discovery methods under a common formulation. SEM introduces an integral-based sparse regression method using Green's functions, enabling derivative-free estimation of differential operators and their associated driving functions in general-order dynamical systems. The effectiveness of SEM is demonstrated through extensive simulations, benchmarking its performance against derivative-based approaches. We then apply SEM to electroencephalographic (EEG) data recorded during multiple oculomotor tasks, collected from 52 participants in a brain-computer interface experiment. Our method identifies active brain regions across participants and reveals task-specific connectivity patterns. These findings offer valuable insights into brain connectivity and the underlying neural mechanisms.

DeepSuM: Deep Sufficient Modality Learning Framework

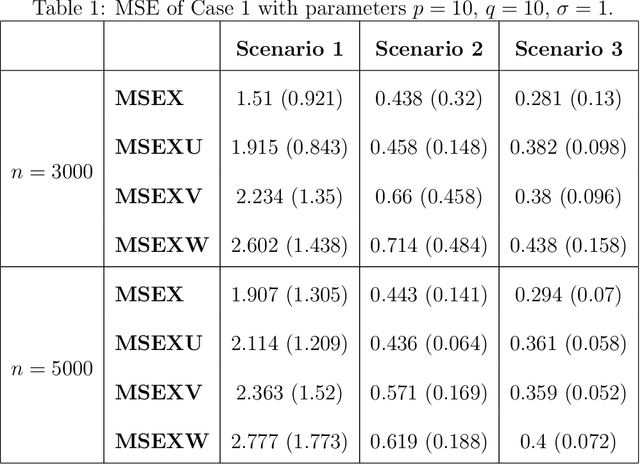
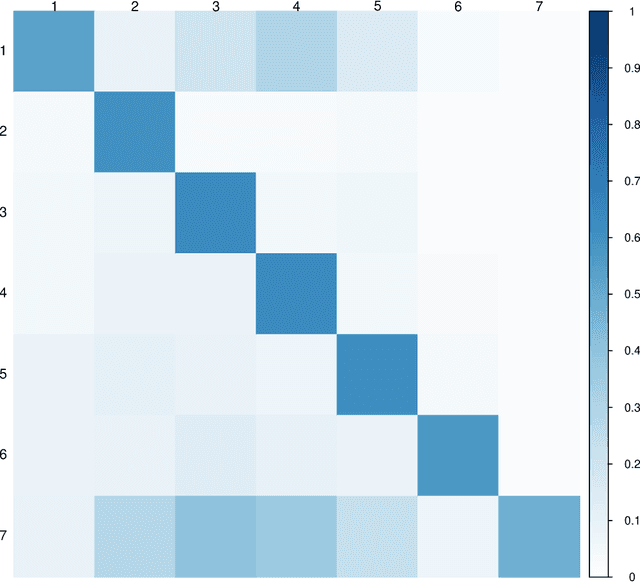
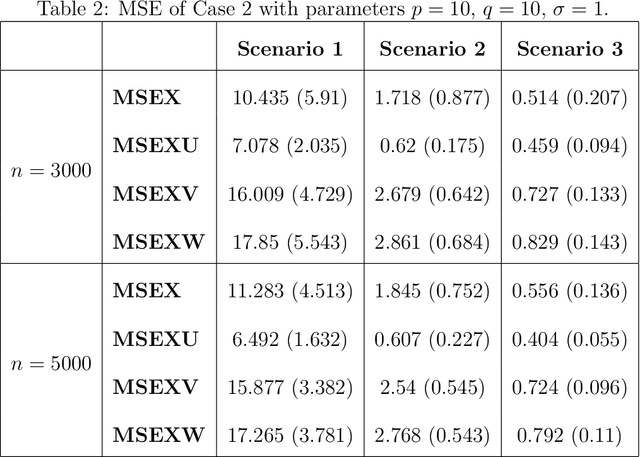
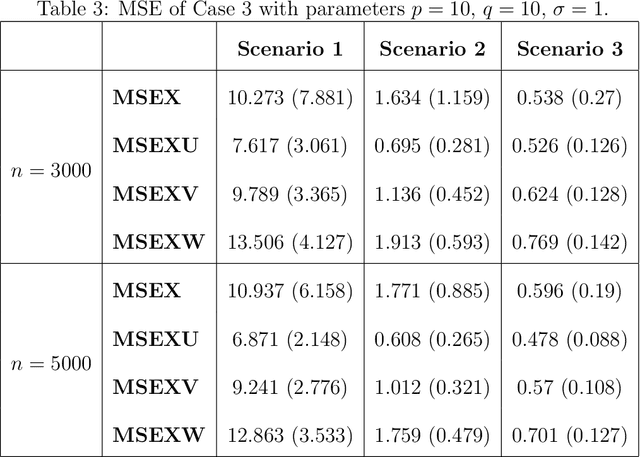
Multimodal learning has become a pivotal approach in developing robust learning models with applications spanning multimedia, robotics, large language models, and healthcare. The efficiency of multimodal systems is a critical concern, given the varying costs and resource demands of different modalities. This underscores the necessity for effective modality selection to balance performance gains against resource expenditures. In this study, we propose a novel framework for modality selection that independently learns the representation of each modality. This approach allows for the assessment of each modality's significance within its unique representation space, enabling the development of tailored encoders and facilitating the joint analysis of modalities with distinct characteristics. Our framework aims to enhance the efficiency and effectiveness of multimodal learning by optimizing modality integration and selection.

Minimax and Communication-Efficient Distributed Best Subset Selection with Oracle Property

The explosion of large-scale data in fields such as finance, e-commerce, and social media has outstripped the processing capabilities of single-machine systems, driving the need for distributed statistical inference methods. Traditional approaches to distributed inference often struggle with achieving true sparsity in high-dimensional datasets and involve high computational costs. We propose a novel, two-stage, distributed best subset selection algorithm to address these issues. Our approach starts by efficiently estimating the active set while adhering to the $\ell_0$ norm-constrained surrogate likelihood function, effectively reducing dimensionality and isolating key variables. A refined estimation within the active set follows, ensuring sparse estimates and matching the minimax $\ell_2$ error bound. We introduce a new splicing technique for adaptive parameter selection to tackle subproblems under $\ell_0$ constraints and a Generalized Information Criterion (GIC). Our theoretical and numerical studies show that the proposed algorithm correctly finds the true sparsity pattern, has the oracle property, and greatly lowers communication costs. This is a big step forward in distributed sparse estimation.

Sparsity-Constraint Optimization via Splicing Iteration

Sparsity-constraint optimization has wide applicability in signal processing, statistics, and machine learning. Existing fast algorithms must burdensomely tune parameters, such as the step size or the implementation of precise stop criteria, which may be challenging to determine in practice. To address this issue, we develop an algorithm named Sparsity-Constraint Optimization via sPlicing itEration (SCOPE) to optimize nonlinear differential objective functions with strong convexity and smoothness in low dimensional subspaces. Algorithmically, the SCOPE algorithm converges effectively without tuning parameters. Theoretically, SCOPE has a linear convergence rate and converges to a solution that recovers the true support set when it correctly specifies the sparsity. We also develop parallel theoretical results without restricted-isometry-property-type conditions. We apply SCOPE's versatility and power to solve sparse quadratic optimization, learn sparse classifiers, and recover sparse Markov networks for binary variables. The numerical results on these specific tasks reveal that SCOPE perfectly identifies the true support set with a 10--1000 speedup over the standard exact solver, confirming SCOPE's algorithmic and theoretical merits. Our open-source Python package skscope based on C++ implementation is publicly available on GitHub, reaching a ten-fold speedup on the competing convex relaxation methods implemented by the cvxpy library.

skscope: Fast Sparsity-Constrained Optimization in Python

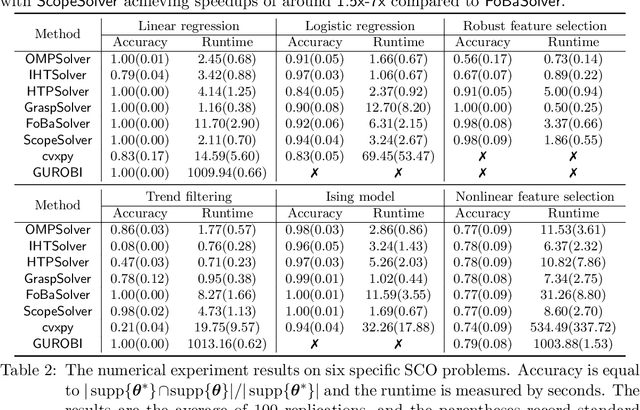
Applying iterative solvers on sparsity-constrained optimization (SCO) requires tedious mathematical deduction and careful programming/debugging that hinders these solvers' broad impact. In the paper, the library skscope is introduced to overcome such an obstacle. With skscope, users can solve the SCO by just programming the objective function. The convenience of skscope is demonstrated through two examples in the paper, where sparse linear regression and trend filtering are addressed with just four lines of code. More importantly, skscope's efficient implementation allows state-of-the-art solvers to quickly attain the sparse solution regardless of the high dimensionality of parameter space. Numerical experiments reveal the available solvers in skscope can achieve up to 80x speedup on the competing relaxation solutions obtained via the benchmarked convex solver. skscope is published on the Python Package Index (PyPI) and Conda, and its source code is available at: https://github.com/abess-team/skscope.

A Consistent and Scalable Algorithm for Best Subset Selection in Single Index Models

Analysis of high-dimensional data has led to increased interest in both single index models (SIMs) and best subset selection. SIMs provide an interpretable and flexible modeling framework for high-dimensional data, while best subset selection aims to find a sparse model from a large set of predictors. However, best subset selection in high-dimensional models is known to be computationally intractable. Existing methods tend to relax the selection, but do not yield the best subset solution. In this paper, we directly tackle the intractability by proposing the first provably scalable algorithm for best subset selection in high-dimensional SIMs. Our algorithmic solution enjoys the subset selection consistency and has the oracle property with a high probability. The algorithm comprises a generalized information criterion to determine the support size of the regression coefficients, eliminating the model selection tuning. Moreover, our method does not assume an error distribution or a specific link function and hence is flexible to apply. Extensive simulation results demonstrate that our method is not only computationally efficient but also able to exactly recover the best subset in various settings (e.g., linear regression, Poisson regression, heteroscedastic models).

Best-Subset Selection in Generalized Linear Models: A Fast and Consistent Algorithm via Splicing Technique

In high-dimensional generalized linear models, it is crucial to identify a sparse model that adequately accounts for response variation. Although the best subset section has been widely regarded as the Holy Grail of problems of this type, achieving either computational efficiency or statistical guarantees is challenging. In this article, we intend to surmount this obstacle by utilizing a fast algorithm to select the best subset with high certainty. We proposed and illustrated an algorithm for best subset recovery in regularity conditions. Under mild conditions, the computational complexity of our algorithm scales polynomially with sample size and dimension. In addition to demonstrating the statistical properties of our method, extensive numerical experiments reveal that it outperforms existing methods for variable selection and coefficient estimation. The runtime analysis shows that our implementation achieves approximately a fourfold speedup compared to popular variable selection toolkits like glmnet and ncvreg.

Simultaneous Best Subset Selection and Dimension Reduction via Primal-Dual Iterations

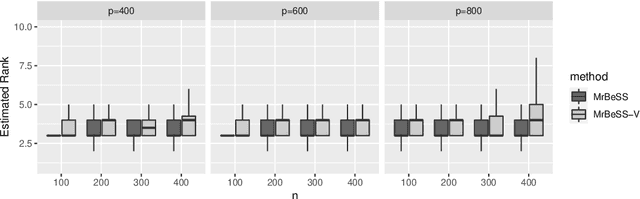
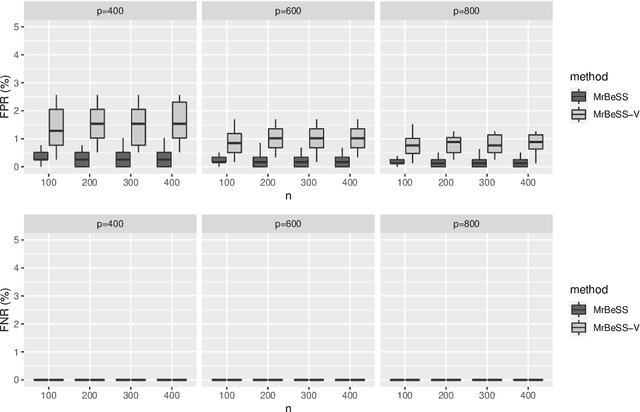
Sparse reduced rank regression is an essential statistical learning method. In the contemporary literature, estimation is typically formulated as a nonconvex optimization that often yields to a local optimum in numerical computation. Yet, their theoretical analysis is always centered on the global optimum, resulting in a discrepancy between the statistical guarantee and the numerical computation. In this research, we offer a new algorithm to address the problem and establish an almost optimal rate for the algorithmic solution. We also demonstrate that the algorithm achieves the estimation with a polynomial number of iterations. In addition, we present a generalized information criterion to simultaneously ensure the consistency of support set recovery and rank estimation. Under the proposed criterion, we show that our algorithm can achieve the oracle reduced rank estimation with a significant probability. The numerical studies and an application in the ovarian cancer genetic data demonstrate the effectiveness and scalability of our approach.

Interpretable travel distance on the county-wise COVID-19 by sequence to sequence with attention

Background: Travel restrictions as a means of intervention in the COVID-19 epidemic have reduced the spread of outbreaks using epidemiological models. We introduce the attention module in the sequencing model to assess the effects of the different classes of travel distances. Objective: To establish a direct relationship between the number of travelers for various travel distances and the COVID-19 trajectories. To improve the prediction performance of sequencing model. Setting: Counties from all over the United States. Participants: New confirmed cases and deaths have been reported in 3158 counties across the United States. Measurements: Outcomes included new confirmed cases and deaths in the 30 days preceding November 13, 2021. The daily number of trips taken by the population for various classes of travel distances and the geographical information of infected counties are assessed. Results: There is a spatial pattern of various classes of travel distances across the country. The varying geographical effects of the number of people travelling for different distances on the epidemic spread are demonstrated. Limitation: We examined data up to November 13, 2021, and the weights of each class of travel distances may change accordingly as the data evolves. Conclusion: Given the weights of people taking trips for various classes of travel distances, the epidemics could be mitigated by reducing the corresponding class of travellers.

abess: A Fast Best Subset Selection Library in Python and R

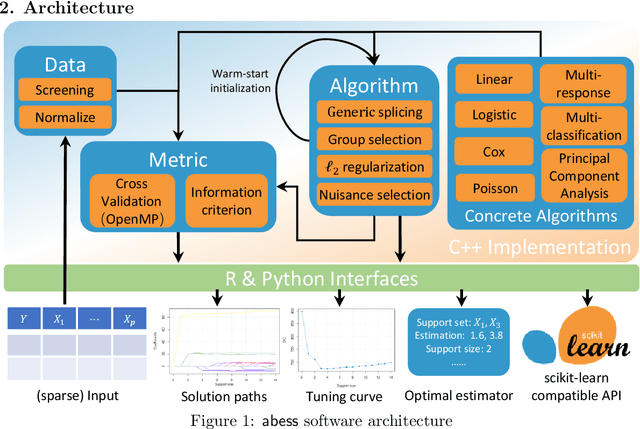
We introduce a new library named abess that implements a unified framework of best-subset selection for solving diverse machine learning problems, e.g., linear regression, classification, and principal component analysis. Particularly, the abess certifiably gets the optimal solution within polynomial times under the linear model. Our efficient implementation allows abess to attain the solution of best-subset selection problems as fast as or even 100x faster than existing competing variable (model) selection toolboxes. Furthermore, it supports common variants like best group subset selection and $\ell_2$ regularized best-subset selection. The core of the library is programmed in C++. For ease of use, a Python library is designed for conveniently integrating with scikit-learn, and it can be installed from the Python library Index. In addition, a user-friendly R library is available at the Comprehensive R Archive Network. The source code is available at: https://github.com/abess-team/abess.