M$^2$FMoE: Multi-Resolution Multi-View Frequency Mixture-of-Experts for Extreme-Adaptive Time Series Forecasting

Forecasting time series with extreme events is critical yet challenging due to their high variance, irregular dynamics, and sparse but high-impact nature. While existing methods excel in modeling dominant regular patterns, their performance degrades significantly during extreme events, constituting the primary source of forecasting errors in real-world applications. Although some approaches incorporate auxiliary signals to improve performance, they still fail to capture extreme events' complex temporal dynamics. To address these limitations, we propose M$^2$FMoE, an extreme-adaptive forecasting model that learns both regular and extreme patterns through multi-resolution and multi-view frequency modeling. It comprises three modules: (1) a multi-view frequency mixture-of-experts module assigns experts to distinct spectral bands in Fourier and Wavelet domains, with cross-view shared band splitter aligning frequency partitions and enabling inter-expert collaboration to capture both dominant and rare fluctuations; (2) a multi-resolution adaptive fusion module that hierarchically aggregates frequency features from coarse to fine resolutions, enhancing sensitivity to both short-term variations and sudden changes; (3) a temporal gating integration module that dynamically balances long-term trends and short-term frequency-aware features, improving adaptability to both regular and extreme temporal patterns. Experiments on real-world hydrological datasets with extreme patterns demonstrate that M$^2$FMoE outperforms state-of-the-art baselines without requiring extreme-event labels.

Simultaneous Best Subset Selection and Dimension Reduction via Primal-Dual Iterations

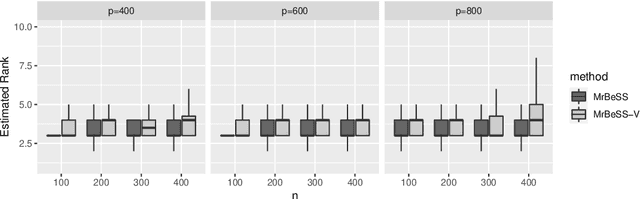
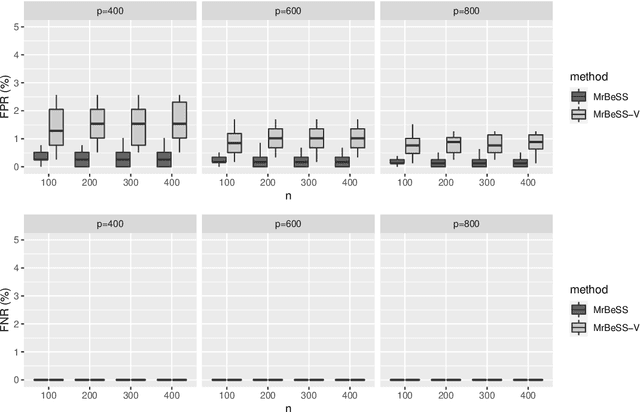
Sparse reduced rank regression is an essential statistical learning method. In the contemporary literature, estimation is typically formulated as a nonconvex optimization that often yields to a local optimum in numerical computation. Yet, their theoretical analysis is always centered on the global optimum, resulting in a discrepancy between the statistical guarantee and the numerical computation. In this research, we offer a new algorithm to address the problem and establish an almost optimal rate for the algorithmic solution. We also demonstrate that the algorithm achieves the estimation with a polynomial number of iterations. In addition, we present a generalized information criterion to simultaneously ensure the consistency of support set recovery and rank estimation. Under the proposed criterion, we show that our algorithm can achieve the oracle reduced rank estimation with a significant probability. The numerical studies and an application in the ovarian cancer genetic data demonstrate the effectiveness and scalability of our approach.

Parallel integrative learning for large-scale multi-response regression with incomplete outcomes

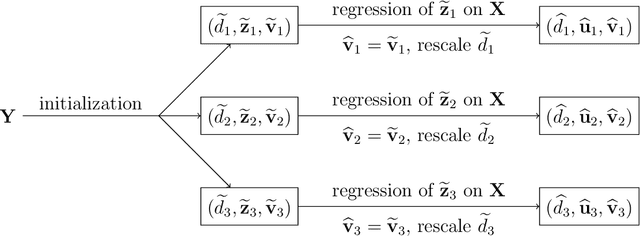
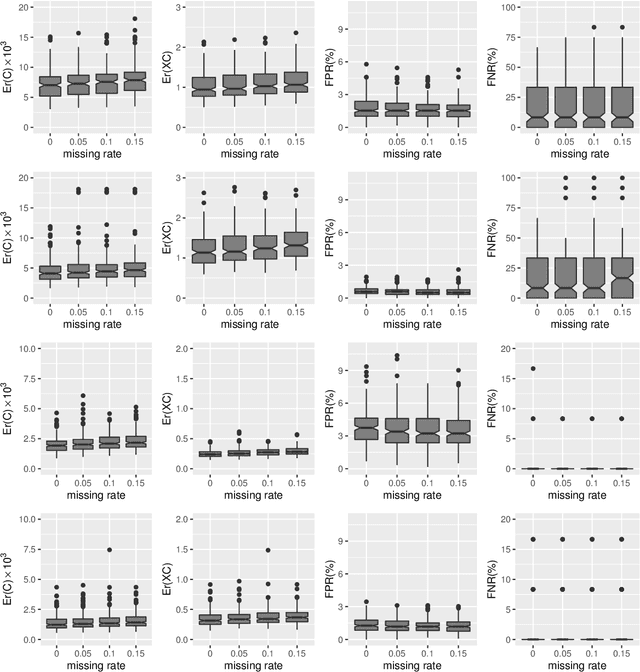
Multi-task learning is increasingly used to investigate the association structure between multiple responses and a single set of predictor variables in many applications. In the era of big data, the coexistence of incomplete outcomes, large number of responses, and high dimensionality in predictors poses unprecedented challenges in estimation, prediction, and computation. In this paper, we propose a scalable and computationally efficient procedure, called PEER, for large-scale multi-response regression with incomplete outcomes, where both the numbers of responses and predictors can be high-dimensional. Motivated by sparse factor regression, we convert the multi-response regression into a set of univariate-response regressions, which can be efficiently implemented in parallel. Under some mild regularity conditions, we show that PEER enjoys nice sampling properties including consistency in estimation, prediction, and variable selection. Extensive simulation studies show that our proposal compares favorably with several existing methods in estimation accuracy, variable selection, and computation efficiency.

Statistically Guided Divide-and-Conquer for Sparse Factorization of Large Matrix

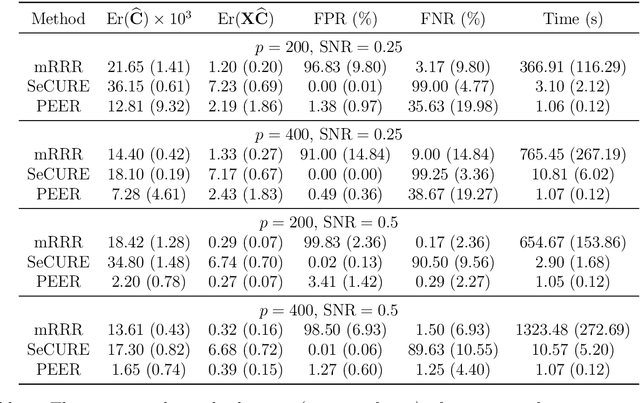
The sparse factorization of a large matrix is fundamental in modern statistical learning. In particular, the sparse singular value decomposition and its variants have been utilized in multivariate regression, factor analysis, biclustering, vector time series modeling, among others. The appeal of this factorization is owing to its power in discovering a highly-interpretable latent association network, either between samples and variables or between responses and predictors. However, many existing methods are either ad hoc without a general performance guarantee, or are computationally intensive, rendering them unsuitable for large-scale studies. We formulate the statistical problem as a sparse factor regression and tackle it with a divide-and-conquer approach. In the first stage of division, we consider both sequential and parallel approaches for simplifying the task into a set of co-sparse unit-rank estimation (CURE) problems, and establish the statistical underpinnings of these commonly-adopted and yet poorly understood deflation methods. In the second stage of division, we innovate a contended stagewise learning technique, consisting of a sequence of simple incremental updates, to efficiently trace out the whole solution paths of CURE. Our algorithm has a much lower computational complexity than alternating convex search, and the choice of the step size enables a flexible and principled tradeoff between statistical accuracy and computational efficiency. Our work is among the first to enable stagewise learning for non-convex problems, and the idea can be applicable in many multi-convex problems. Extensive simulation studies and an application in genetics demonstrate the effectiveness and scalability of our approach.